
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由已知以$\overrightarrow{a}$,$\overrightarrow{b}$为邻边的四边形对角线相等,所以是矩形,利用一边与对角线长度为2倍关系得到所求.
解答  解:若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|=2|{\overrightarrow a}|$,则以$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$为邻边的四边形OACB的对角线相等,
解:若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|=2|{\overrightarrow a}|$,则以$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$为邻边的四边形OACB的对角线相等,
所以OACB是矩形,
并且OC=|$\overrightarrow{a}+\overrightarrow{b}$|=2|$\overrightarrow{a}$|=2OA,即对角线是一边的2倍,所以向量$\overrightarrow{OC}$=$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$=$\overrightarrow{OA}$的夹角为$\frac{π}{3}$,
即∠AOC=$\frac{π}{3}$,
则向量$\overrightarrow{BA}$=$\overrightarrow a-\overrightarrow b$与$\overrightarrow{OB}$=$\overrightarrow b$的夹角为π-$\frac{π}{6}$=$\frac{5π}{6}$,
故选:D.
点评 本题考查了向量的平行四边形法则及几何意义的运用,关键是由已知判断四边形的形状,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{{{n^2}+n}}{2}$ | B. | an=$\frac{{{n^2}-n}}{2}$ | C. | an=n2-n+1 | D. | an=n2+n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
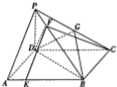 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com