
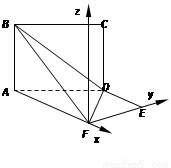
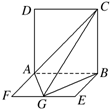
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形, AF∥DE,AF⊥FE,AF=AD=2 DE=2.
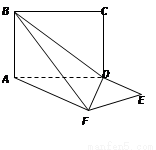
(Ⅰ) 求异面直线EF与BC所成角的大小;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为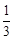 ,求AB的长.
,求AB的长.
(Ⅰ) 30°(Ⅱ) 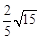
【解析】
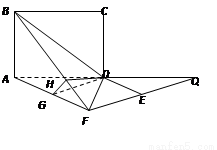
试题分析: (Ⅰ) 延长AD,FE交于Q.
因为ABCD是矩形,所以
BC∥AD,
所以∠AQF是异面直线EF与BC所成的角.
在梯形ADEF中,因为DE∥AF,AF⊥FE,AF=2,DE=1得
∠AQF=30°.即异面直线EF与BC所成角的大小为30°. 7分
(Ⅱ) 方法一:
设AB=x.取AF的中点G.由题意得DG⊥AF.
因为平面ABCD⊥平面ADEF,AB⊥AD,所以AB⊥平面ADEF,
所以AB⊥DG.所以DG⊥平面ABF.
过G作GH⊥BF,垂足为H,连结DH,则DH⊥BF,
所以∠DHG为二面角A-BF-D的平面角.
在直角△AGD中,AD=2,AG=1,得DG=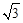 .
.
在直角△BAF中,由 =sin∠AFB=
=sin∠AFB=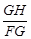 ,得
,得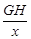 =
=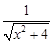 ,
,
所以GH=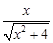 .
.
在直角△DGH中,DG=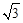 ,GH=
,GH=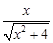 ,得DH=
,得DH=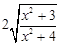 .
.
因为cos∠DHG=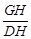 =
=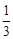 ,得x=
,得x=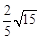 ,
,
所以AB=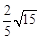 .
15分
.
15分
方法二:设AB=x.
以F为原点,AF,FQ所在的直线分别为x轴,y轴建立空间直角坐标系Fxyz.则
F(0,0,0),A(-2,0,0),E(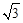 ,0,0),D(-1,
,0,0),D(-1,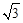 ,0),B(-2,0,x),
,0),B(-2,0,x),
所以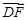 =(1,-
=(1,-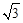 ,0),
,0),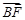 =(2,0,-x).
=(2,0,-x).
因为EF⊥平面ABF,所以平面ABF的法向量可取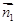 =(0,1,0).
=(0,1,0).
设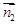 =(x1,y1,z1)为平面BFD的法向量,则
=(x1,y1,z1)为平面BFD的法向量,则
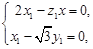
所以,可取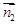 =(
=(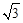 ,1,
,1,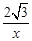 ).
).
因为cos<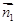 ,
,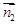 >=
>=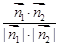 =
=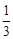 ,得x=
,得x=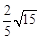 ,
,
所以AB=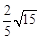 .
15分
.
15分
考点:本题主要考查空间点、线、面位置关系,异面直线所成角、二面角等基础知识,空间向量的应用,同时考查空间想象能力和运算求解能力。
点评:如何用传统的方法求解此类问题,要紧扣相应的判定定理和性质定理,还要注意各类角的取值范围;如果用空间向量求解,思路比较简单,但是运算比较复杂,要仔细运算.


科目:高中数学 来源: 题型:
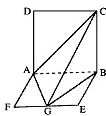 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.查看答案和解析>>
科目:高中数学 来源: 题型:
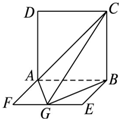 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com