解:(1)因为f(x+2)=f[(x+1)+1]=-f(x+1)=-[-f(x)]=f(x)
所以:2是函数f(x)的一个周期(2分)
(2)∵f(x)是以2为周期的函数,即f(x-2k)=f(x),k∈Z
设x∈[2k-1,2k+1],则x-2k∈[-1,1]∴f(x-2k)=(x-2k)
2,
即f(x)=(x-2k)
2,x∈[2k-1,2k+1](k∈Z)(6分)
(3)当x∈[2k-1,2k+1]时,
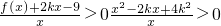
①当k≥1时,则2k-1≥1,∴x>0
∴原题等价于x
2-2kx+4k
2-9>0对任意x∈[2k-1,2k+1]恒成立.
设g(x)=x
2-2kx+4k
2-9
当k≥1时,对称轴x=k≤2k-1
则g(2k-1)=4k
2-2k-8≥0,
解得
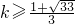
或
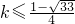
∴整数k≥2(10分)
②当k≤-1时,则2k+1≤-1,∴x<0,
∴原题等价于x
2-2kx+4k
2-9<0对任意x∈[2k-1,2k+1]恒成立,
设g(x)=x
2-2kx+4k
2-9
当k≤-1时,对称轴x=k≥2k+1
则g(2k-1)=4k
2-2k-8>0,
解得
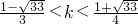
∴整数k=-1(14分)
③当k=0时,原命题等价于
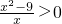
对任意x∈[-1,1]恒成立
当x=1时,则-8>0显然不成立∴k≠0(15分)
综上所述,所求k的取值范围是[2,+∞)∪-1.(16分)
分析:(1)因为f(x+2)=f[(x+1)+1]=-f(x+1)=-[-f(x)]=f(x)可得结论.
(2)设x∈[2k-1,2k+1],则x-2k∈[-1,1]∵f(x)是以2为周期的函数,即f(x-2k)=f(x)可求解.
(3)当x∈[2k-1,2k+1]时,
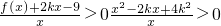
恒成立,再用二次函数法求解.
点评:本题主要考查函数的周期性及用周期性求函数解析式,这类问题要注意转化自变量所在区间是关键.还考查了恒成立问题,要通过函数类型来求最值解决,本题用的是二次函数法,对称轴与区间的相对位置,即研究了单调性,也明确了自变量的正负,题目设计可谓巧妙.

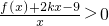 对任意x∈[2k-1,2k+1]恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
对任意x∈[2k-1,2k+1]恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.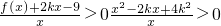
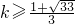 或
或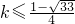 ∴整数k≥2(10分)
∴整数k≥2(10分)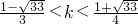 ∴整数k=-1(14分)
∴整数k=-1(14分)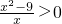 对任意x∈[-1,1]恒成立
对任意x∈[-1,1]恒成立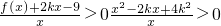 恒成立,再用二次函数法求解.
恒成立,再用二次函数法求解.

 已知定义在R上的偶函数f(x).当x≥0时,f(x)=
已知定义在R上的偶函数f(x).当x≥0时,f(x)=