
【题目】已知函数f(x)=ln(1+x)﹣x,g(x)=xlnx.
(1)求函数f(x)的最大值;
(2)设0<a<b,证明0<g(a)+g(b)﹣2g( ![]() )<(b﹣a)ln2.
)<(b﹣a)ln2.
【答案】
(1)解:函数f(x)的定义域为(﹣1,+∞).
![]() .令f′(x)=0,解得x=0.
.令f′(x)=0,解得x=0.
当﹣1<x<0时,f′(x)>0,当x>0时,f′(x)<0.又f(0)=0,
故当且仅当x=0时,f(x)取得最大值,最大值为0.
(2)证明: ![]()
= ![]() .
.
由(Ⅰ)结论知ln(1+x)﹣x<0(x>﹣1,且x≠0),
由题设 ![]() ,
,
因此ln ![]() =﹣ln(1+
=﹣ln(1+ ![]() )>﹣
)>﹣ ![]() ,
,
![]() ,
,
所以 ![]() .
.
又 ![]() ,
,
![]() <
< ![]() .=(b﹣a)ln
.=(b﹣a)ln ![]() <(b﹣a)ln2
<(b﹣a)ln2
综上 ![]()
【解析】(1)先求出函数的定义域,然后对函数进行求导运算,令导函数等于0求出x的值,再判断函数的单调性,进而可求出最大值.(2)先将a,b代入函数g(x)得到g(a)+g(b)﹣2g( ![]() )的表达式后进行整理,根据(1)可得到lnx<x,将
)的表达式后进行整理,根据(1)可得到lnx<x,将 ![]() 、
、 ![]() 放缩变形为
放缩变形为 ![]() 、
、 ![]() 代入即可得到左边不等式成立,再用
代入即可得到左边不等式成立,再用 ![]() 根据y=lnx的单调性进行放缩
根据y=lnx的单调性进行放缩 ![]() <
< ![]() .然后整理即可证明不等式右边成立.
.然后整理即可证明不等式右边成立.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 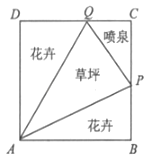
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点.求:
(1)当|OA|十|OB|取得最小值时,直线l的方程;
(2)当|MA|2+|MB|2取得最小值时,直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数f(x)与g(x)的图象相同的是( )
A.f(x)=x,g(x)=( ![]() )2
)2
B.f(x)=x2 , g(x)=(x+1)2
C.f(x)=1,g(x)=x0
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),如果存在非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,已知函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[﹣1,1]时,f(x)=x2 , 则y=f(x)与y=log5x的图象的交点个数为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2﹣6x+5≤0,q:x2﹣2x+1﹣m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q. 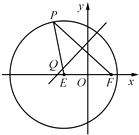
(1)求动点Q的轨迹Γ的方程;
(2)设直线l与(1)中轨迹Γ相交于A,B两点,直线AO,l,OB的斜率分别为k1 , k,k2(其中k>0),若k1 , k,k2恰好构成公比不为1的等比数列,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失. 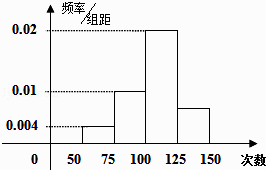
(Ⅰ) 已知第1小组频数为10,求参加这次测试的人数?
(Ⅱ) 求第4小组在y轴上的对应值;
(Ⅲ) 若次数在75次以上 ( 含75次 ) 为达标,试估计该年级跳绳测试达标率是多少?
(Ⅳ) 试估计这些数据的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com