
分析 (1)求出导函数F'(x),根据题意对参数a分类讨论,分别求函数的最小值判断得出a的取值;
(2)把恒成立问题转化为最值问题,通过构造函数,利用导函数求出函数的最值即可.
解答 解:(1)$F(x)=f(x)+g(x)-x=lnx+\frac{a}{x}$,其定义域为{x|x>0},
则$F'(x)=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2},x>0$
①若a≤1,则对x∈[1,e],F'(x)≥0恒成立,
故F(x)在[1,e]上单调递增F(x)min=F(1)=a≤1,与题意矛盾,舍去
②若1<a<e,则F(x)在[1,a]上单调递减,在[a,e]上单调递增,$F{(x)_{min}}=F(a)=1+lna=\frac{3}{2}⇒a=\sqrt{e}$,符合题意
③若a≥e,则则F(x)在[1,e]上单调递减,$F{(x)_{min}}=F(e)=1+\frac{a}{e}≥2$,矛盾,舍去
综上:$a=\sqrt{e}$
(2)由题设可得:x≥1时,$lnx≤x+\frac{a}{x}$恒成立,等价于a≥(xlnx-x2)max
令h(x)=xlnx-x2,x≥1,
则$h'(x)=1+lnx-2x,h''(x)=\frac{1}{x}-2<0$,
故h'(x)在[1,+∞)上单调递减,
∴h'(x)≤h'(1)=-1<0,
∴h(x)在[1,+∞)上单调递减,
∴h(x)max=h(1)=-1
∴a≥-1
点评 考查了函数的构造,导函数的应用,参数的讨论和恒成立问题的转化思想.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:解答题
已知集合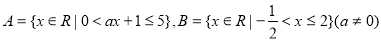 .
.
(1)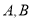 能否相等?若能,求出实数
能否相等?若能,求出实数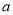 的值;若不能,试说明理由;
的值;若不能,试说明理由;
(2)若命题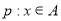 ,命题
,命题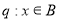 ,且
,且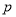 是
是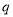 充分不必要条件,求实数
充分不必要条件,求实数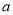 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
设数列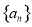 的前
的前 项和为
项和为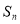 ,且
,且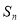
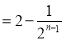 ,
,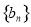 为等差数列,且
为等差数列,且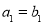 ,
,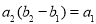 .
.
(1)求数列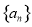 和
和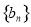 通项公式;
通项公式;
(2)设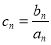 ,求数列
,求数列 的前
的前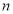 项和
项和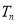 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: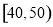 ,
,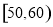 ,…,
,…,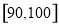 后得到如下频率分布直方图.
后得到如下频率分布直方图.
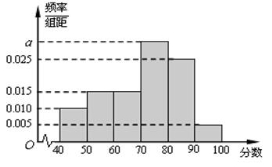
(Ⅰ)求分数在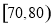 内的频率;
内的频率;
(Ⅱ)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(Ⅲ)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com