
【题目】若抛物线y2=2px(p>0)上一点到焦点和抛物线对称轴的距离分别为10和6,则抛物线方程为( )
A.y2=4x
B.y2=36x
C.y2=4x或y2=36x
D.y2=8x或y2=32x
科目:高中数学 来源: 题型:
【题目】生产某种产品的年固定成本为250万元,每生产x千件,需要另投入成本为C(x),当年产量不足80千件时,C(x)= ![]() +20x(万元),当年产量不小于80千件时,C(x)=51x+
+20x(万元),当年产量不小于80千件时,C(x)=51x+ ![]() ﹣1450(万元),通过市场分析,每件商品售价为0.05万元时,该商品能全部售完.
﹣1450(万元),通过市场分析,每件商品售价为0.05万元时,该商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式(利润=销售额﹣成本);
(2)年产量为多少千件时,生产该商品获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =
=![]() =
= ![]() .
.
(1)求函数![]() 的单调递增区间;(只需写出结论即可)
的单调递增区间;(只需写出结论即可)
(2)设函数![]() =
= ![]() ,若
,若![]() 在区间
在区间![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(![]() +x)cos(
+x)cos(![]() -x),g(x)=
-x),g(x)=![]() sin 2x-
sin 2x-![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE= ![]() CD=2,M是线段AE上的动点.
CD=2,M是线段AE上的动点. 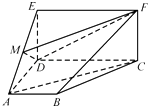
(Ⅰ)试确定点M的位置,使AC∥平面MDF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面MDF将几何体ADE﹣BCF分成的两部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了50名女性和50名男性,根据调研结果得到如图所示的等高条形图
(1)完成下列2×2列联表:
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关” 附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)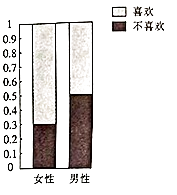
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对正整数n,记In={1,2,3,...,n},Pn={![]() |m∈In,k∈In}.
|m∈In,k∈In}.
(1)求集合P7中元素的个数;
(2)若Pn的子集A中任意两个元素之和不是整数的平方,则称A为“稀疏集”.求n的最大值,使Pn能分成两个不相交的稀疏集的并集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com