
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .直线
.直线![]() 与
与![]() 轴正半轴和
轴正半轴和![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与椭圆分别交于点
,与椭圆分别交于点![]() 、
、![]() ,各点均不重合且满足
,各点均不重合且满足![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)若![]() ,试证明:直线
,试证明:直线![]() 过定点并求此定点.
过定点并求此定点.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地对产品进行抽查检测,现对某条生产线上随机抽取的100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
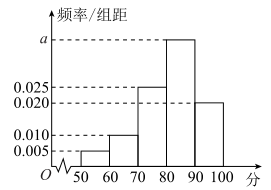
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,视频率作为概率,在该条生产线中随机抽取3个产品,求所抽取的产品中一等品数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右焦点到渐近线的距离为3.现有如下条件:①双曲线
的右焦点到渐近线的距离为3.现有如下条件:①双曲线![]() 的离心率为
的离心率为![]() ; ②双曲线
; ②双曲线![]() 与椭圆
与椭圆![]() 共焦点; ③双曲线右支上的一点
共焦点; ③双曲线右支上的一点![]() 到
到![]() 的距离之差是虚轴长的
的距离之差是虚轴长的![]() 倍.
倍.
请从上述3个条件中任选一个,得到双曲线![]() 的方程为_____________.
的方程为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,射线![]() 与圆
与圆![]() 交于点
交于点![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴正半轴建立平面直角坐标系
轴正半轴建立平面直角坐标系![]()
(1)求点![]() 的直角坐标和椭圆
的直角坐标和椭圆![]() 的参数方程;
的参数方程;
(2)若![]() 为椭圆
为椭圆![]() 的下顶点,
的下顶点,![]() 为椭圆
为椭圆![]() 上任意一点,求
上任意一点,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx-bx2,a,b∈R.若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,则实数a的取值范围是( )
A. [e,+∞)B. [![]() ,+∞)
,+∞)
C. [![]() ,e2)D. [e2,+∞)
,e2)D. [e2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com