
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,满足
上,满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 过点
过点![]() ,且与椭圆只有一个公共点,直线
,且与椭圆只有一个公共点,直线![]() 与
与![]() 的倾斜角互补,且与椭圆交于异于点
的倾斜角互补,且与椭圆交于异于点![]() 的两点
的两点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() (
(![]() 介于
介于![]() ,
,![]() 两点之间).
两点之间).
(i)求证:![]() ;
;
(ii)是否存在直线![]() ,使得直线
,使得直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率按某种顺序能构成等比数列?若能,求出
的斜率按某种顺序能构成等比数列?若能,求出![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
【答案】(1)![]() (2)(i)见解析(ii)
(2)(i)见解析(ii)![]()
【解析】试题分析:
(1)设![]() ,由题意可得
,由题意可得![]() ,所以
,所以![]() . 结合椭圆的定义可得
. 结合椭圆的定义可得![]() . 则椭圆C的标准方程为
. 则椭圆C的标准方程为![]() .
.
(2)(ⅰ)设![]() 方程为
方程为![]() ,与
,与![]() 联立可得
联立可得![]() . 则
. 则![]() 的斜率是
的斜率是![]() .
.
联立直线![]() 方程与椭圆方程,结合韦达定理可得
方程与椭圆方程,结合韦达定理可得![]()
![]() ,
,![]() 和
和![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,![]() ,结合几何关系可得
,结合几何关系可得![]() 成立.
成立.
(ⅱ)由(ⅰ)知,![]() ,
,![]() ,
,![]() .假设存在直线
.假设存在直线![]() ,满足题意.不妨设
,满足题意.不妨设![]() ,
,![]() ,
,![]() 若
若![]() 按某种排序构成等比数列,则
按某种排序构成等比数列,则![]() ,则
,则![]() ,此时直线
,此时直线![]() 与
与![]() 平行或重合,与题意不符,则不存在直线
平行或重合,与题意不符,则不存在直线![]() 满足题意.
满足题意.
试题解析:
(1)设![]() ,
,
则![]() =
=![]() ,所以
,所以![]() .
.
因为![]() =4,所以
=4,所以![]() .
. ![]()
故椭圆C的标准方程为![]() .
.
(2)(ⅰ)设![]() 方程为
方程为![]() ,与
,与![]() 联立,消
联立,消![]() 得
得
![]() , 由题意知
, 由题意知![]() ,解得
,解得![]() .
.
因为直线![]() 与
与![]() 的倾斜角互补,所以
的倾斜角互补,所以![]() 的斜率是
的斜率是![]() .
.
设直线![]() 方程:
方程:![]() ,
,![]() ,联立
,联立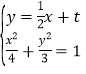 ,整理得
,整理得![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,
,![]() ;
;
直线![]() 、
、![]() 的斜率之和
的斜率之和
![]()
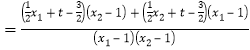
![]()
![]()
所以![]() 关于直线
关于直线![]() 对称,即
对称,即![]() ,
,
在![]() 和
和![]() 中,由正弦定理得
中,由正弦定理得
![]() ,
,![]() ,
,
又因为![]() ,
,![]()
所以![]()
故![]() 成立.
成立.
(ⅱ)由(ⅰ)知,![]() ,
,![]() ,
,![]() .
.
假设存在直线![]() ,满足题意.不妨设
,满足题意.不妨设![]() ,
,![]() ,
,![]() 若
若![]() 按某种排序构成等比数列,设公比为
按某种排序构成等比数列,设公比为![]() ,则
,则![]() 或
或![]() 或
或![]() .
.
所以![]() ,则
,则![]() ,此时直线
,此时直线![]() 与
与![]() 平行或重合,与题意不符,
平行或重合,与题意不符,
故不存在直线![]() ,满足题意.
,满足题意.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l:  (t为参数)与曲线C相交于M,N两点.
(t为参数)与曲线C相交于M,N两点.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于实数x的一元二次方程![]() .
.
![]() Ⅰ
Ⅰ![]() 若a是从区间
若a是从区间![]() 中任取的一个整数,b是从区间
中任取的一个整数,b是从区间![]() 中任取的一个整数,求上述方程有实根的概率.
中任取的一个整数,求上述方程有实根的概率.
![]() Ⅱ
Ⅱ![]() 若a是从区间
若a是从区间![]() 任取的一个实数,b是从区间
任取的一个实数,b是从区间![]() 任取的一个实数,求上述方程有实根的概率.
任取的一个实数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| a |
|
第3组 |
| 30 | b |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
| |
![]() Ⅰ
Ⅰ![]() 求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
![]() Ⅱ
Ⅱ![]() 根据样本频率分布直方图估计样本成绩的中位数;
根据样本频率分布直方图估计样本成绩的中位数;
![]() Ⅲ
Ⅲ![]() 高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.
高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黑板上写有,1,2,…,666,这666个正整数,第一步划去最前面的八个数:1,2,…,8,,并在666后面写上1,2,…,8的和36;第二步再划去最前面的八个数:9,10,…,16,并在最后面写上9,10,…,16的和100;如此继续下去(即每一步划去最前面的八个数,并在最后写上划去的八个数的和).
(1)问:经过多少步后,黑板上只剩下一个数?
(2)当黑板上只剩下一个数时,求出在黑板上出现过的所有数的和(如果一个数多次出现需重复计算).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() .
.
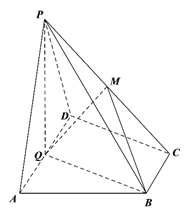
(Ⅰ)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若二面角![]() 为
为![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为![]() ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别![]() ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.
(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com