
【题目】如图所示的算法流程图中,输出S的值为( ) 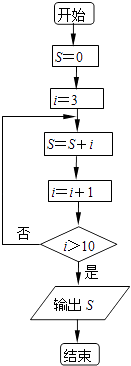
A.32
B.42
C.52
D.63
【答案】C
【解析】解:运行算法,可得:
第一次S=3,i=4,i<10;
第二次S=3+4,i=5,i<10;
第三次S=3+4+5,i=6,i<10;
第四次S=3+4+5+6,i=7,i<10;
第五次S=3+4+5+6+7,i=8,i<10;
第六次S=3+4+5+6+7+8,i=9,i<10;
第七次S=3+4+5+6+7+8+9,i=10,i=10;
第八次S=3+4+5+6+7+8+9+10,i=11,i>10;
满足判断框中的条件,结束循环,此时输出S=52,
故选:C.
【考点精析】解答此题的关键在于理解程序框图的相关知识,掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D是BC的中点. 
(1)若E为B1C1的中点,求证:BE∥平面AC1D;
(2)若平面B1BCC1⊥平面ABC,且AB=AC,求证:平面AC1D⊥平面B1BCC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用a代表红球,b代表蓝球,c代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由(1+a)(1+b)的展开式1+a+b+ab表示出来,如:“1”表示一个球都不取、“a”表示取出一个红球,而“ab”表示把红球和蓝球都取出来,以此类推,下列各式中,其展开式可用来表示从3个无区别的红球、3个无区别的蓝球、2个有区别的黑球中取出若干个球,且所有蓝球都取出或都不取出的所有取法的是
①(1+a+a2+a3)(1+b3)(1+c)2
②(1+a3)(1+b+b2+b3)(1+c)2
③(1+a)3(1+b+b2+b3)(1+c2)
④(1+a3)(1+b)3(1+c+c2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(θ为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=﹣2.
(1)求C1和C2在直角坐标系下的普通方程;
(2)已知直线l:y=x和曲线C1交于M,N两点,求弦MN中点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆M:![]() 的左顶点为
的左顶点为![]() 、中心为
、中心为![]() ,若椭圆M过点
,若椭圆M过点![]() ,且
,且![]()
![]() .
.
(1)求椭圆M的方程;
(2)若△APQ的顶点Q也在椭圆M上,试求△APQ面积的最大值;
(3)过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交椭圆M于
的直线交椭圆M于![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 恒过一个定点.
恒过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x﹣1)2+(y﹣3)2=1,圆C2:(x﹣6)2+(y﹣1)2=1,M,N分别是圆C1 , C2上的动点,P为直线x﹣y﹣2=0上的动点,则||PM|﹣|PN||的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
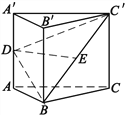
【题目】如图,正三棱柱![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一点,
上的一点,![]() .
.
(1)若![]() 平面
平面![]() ,求证:
,求证:![]() .
.
(2)平面![]() 将棱柱
将棱柱![]() 分割为两个几何体,记上面一个几何体的体积为
分割为两个几何体,记上面一个几何体的体积为![]() ,下面一个几何体的体积为
,下面一个几何体的体积为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=2n2+n,n∈N* .
(1)求{an}的通项公式;
(2)若数列{bn}满足an=4log2bn+3,n∈N* , 求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边长分别为a,b,c且满足csinA= ![]() acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
A.1
B.![]()
C.3
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com