
| A. | 8733 | B. | 8710 | C. | 8726 | D. | 8717 |
分析 通过前2项及an+2是anan+1的个位数字写出前几项的值,可知该数列的周期为6,进而可得结论.
解答 解:∵a1=1,a2=3,
∴a1a2=1•3=3,
又∵an+2是anan+1的个位数字,
∴a3=3,
∵a2a3=3•3=9,∴a4=9,
∵a3a4=3•9=27,∴a5=7,
∵a4a5=9•7=63,∴a6=3,
∵a5a6=7•3=21,∴a7=1,
∴该数列是以6为周期的周期数列,
且前6项和为1+3+3+9+7+3=26,
∵2015=336•6-1,
∴S2015=336•26-3=8736-3=8733,
故选:A.
点评 本题考查数列的通项,找出周期是解决本题的关键,注意解题方法的积累,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
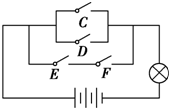 一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 333 | B. | 336 | C. | 1678 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
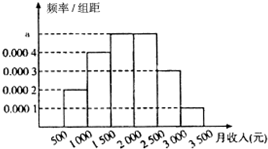 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com