
【题目】如图所示四棱锥![]() 的底面为正方形,
的底面为正方形,![]() 平面
平面![]() 则下列结论中不正确的是( )
则下列结论中不正确的是( )

A.![]() B.
B.![]() 平面
平面![]()
C.直线![]() 与平面
与平面![]() 所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
【答案】C
【解析】
根据空间中垂直关系的判定和性质,平行关系的判定和性质,以及线面角的相关知识,对选项进行逐一判断即可.
对A:因为底面ABCD为正方形,故AC![]() BD,
BD,
又SD![]() 底面ABCD,AC
底面ABCD,AC![]() 平面ABCD,故SD
平面ABCD,故SD![]() AC,
AC,
又BD![]() 平面SBD,SD
平面SBD,SD![]() 平面SBD,故AC
平面SBD,故AC![]() 平面SBD,
平面SBD,
又SB![]() 平面SBD,故AC
平面SBD,故AC![]() .
.
故A正确;
对B:因为底面ABCD为正方形,故AB//CD,
又CD![]() 平面SCD,故AB//平面SCD.
平面SCD,故AB//平面SCD.
故B正确.
对C:由A中推导可知AC![]() 平面SBD,故取AC与BD交点为O,连接SO,如图所示:
平面SBD,故取AC与BD交点为O,连接SO,如图所示:

则![]() 即为所求线面角,但该三角形中边长关系不确定,
即为所求线面角,但该三角形中边长关系不确定,
故线面角的大小不定,
故C错误;
对D:由AC![]() 平面SBD,故取AC与BD交点为O,连接SO,
平面SBD,故取AC与BD交点为O,连接SO,
则![]() 即为SA和SC与平面SBD所成的角,
即为SA和SC与平面SBD所成的角,
因为![]() ,故
,故![]() ,
,
故D正确.
综上所述,不正确的是C.
故选:C.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海的国家会展中心举办.国家展、企业展、经贸论坛、高新产品汇集……首届进博会高点纷呈.一个更加开放和自信的中国,正用实际行动为世界构筑共同发展平台,展现推动全球贸易与合作的中国方案.
某跨国公司带来了高端智能家居产品参展,供购商洽谈采购,并决定大量投放中国市场.已知该产品年固定研发成本30万美元,每生产一台需另投入90美元.设该公司一年内生产该产品![]() 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为![]() 万美元,
万美元,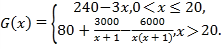
(1)写出年利润![]() (万美元)关于年产量
(万美元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有5人进入到一列有7节车厢的地铁中,分别求下列情况的概率![]() 用数字作最终答案
用数字作最终答案![]() :
:
![]() 恰好有5节车厢各有一人;
恰好有5节车厢各有一人;
![]() 恰好有2节不相邻的空车厢;
恰好有2节不相邻的空车厢;
![]() 恰好有3节车厢有人.
恰好有3节车厢有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是_________.
(1)命题“若![]() ,则方程
,则方程![]() 有实数根”的逆否命题为“若方程
有实数根”的逆否命题为“若方程![]() 无实数根,则
无实数根,则![]() ”.
”.
(2)命题“![]() ,
,![]() ”的否定“
”的否定“![]() ,
,![]() ”.
”.
(3)若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题.
均为假命题.
(4)“![]() ”是“直线
”是“直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行”的充要条件.
平行”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 、
、![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题中真命题的是( )
①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量平均增加0.4个单位;
每增加一个单位时,预报变量平均增加0.4个单位;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理科)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为 “课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为 “课外体育达标”与性别有关?

(2)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的数学期望.
的数学期望.
独立性检验界值表:

(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com