用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（ ）
| A．假设三内角都不大于60度 |
| B．假设三内角都大于60度 |
| C．假设三内角至多有一个大于60度 |
| D．假设三内角至多有两个大于60度 |
阅读快车系列答案科目：高中数学 来源： 题型：单选题
图1，2，3，4分别包含1，5，13和25个互不重叠的单位正方形，按同样的方式构造图形，则第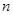
个图包含______个互不重叠的单位正方形。
图1 图2 图3 图4
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
①由“若a，b，c∈R，则(ab)c＝a(bc)”类比“若a、b、c为三个向量，则(a·b)c＝a(b·c)”；
②在数列{an}中，a1＝0，an＋1＝2an＋2，猜想an＝2n－2；
③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”；
上述三个推理中，正确的个数为( )
| A．0 | B．1 | C．2 | D．3 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
法国数学家费马观察到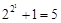
，
，
，
都是质数，于是他提出猜想：任何形如
N*）的数都是质数，这就是著名的费马猜想. 半个世纪之后，善于发现的欧拉发现第5个费马数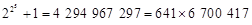
不是质数，从而推翻了费马猜想，这一案例说明( )
| A．归纳推理，结果一定不正确 | B．归纳推理，结果不一定正确 |
| C．类比推理，结果一定不正确 | D．类比推理，结果不一定正确 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
用反证法证明命题：“若整系数一元二次方程
有有理根，那么
中至少有一个是偶数时，下列假设中正确的是
| A．假设都是偶数 |
| B．假设都不是偶数 |
| C．假设至多有一个是偶数 |
| D．假设至多有两个是偶数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则对于
，
．
，则
”类推出“若
，则
”类推出“
” 
（
）” 
” 类推出“
” 
的值的一个程序框图，其中判断框内应填入
＋
，Q＝
＋
(a≥0)，则P，Q的大小关系( )