练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过定点任作互相垂直的两条直线和，分别与轴轴交于两点，线段中点为，则的最小值为__________.

    【答案】

    【解析】

    通过当l1不平行于坐标轴时，设l1：y﹣2＝k（x﹣4），l2：y﹣2（x﹣4），求出A，B的

    坐标，设AB的中点P（x，y），消去k得轨迹方程，当l1平行于坐标轴时，判断是否满足方程．再利用点到直线的距离求解.

    当l1不平行于坐标轴时，设l1：y﹣2＝k（x﹣4） ①

    则l2：y﹣2（x﹣4） ②

    在①中令y＝0得，A（4，0），在②中令x＝0得，B（0，2）．

    设AB的中点P（x，y），则，消去k得，2x+y﹣5＝0，

    当l1平行于坐标轴时，AB的中点为（2，1）也满足此方程．

    ∴P点的轨迹方程为2x+y﹣5＝0．

    所以|OP|=.

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】数列
    （1）在等差数列{an}中，a6=10，S5=5，求该数列的第8项a8；
    （2）在等比数列{bn}中，b1+b3=10，b4+b6= ，求该数列的前5项和S5 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在同一个坐标系中画出函数y=ax ， y=sinax的部分图象，其中a＞0且a≠1，则下列所给图象中可能正确的是（　　）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知点P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点．

    （1）求证：MN∥平面PAD；

    （2）在PB上确定一个点Q，使平面MNQ∥平面PAD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC—A1B1C1中，AC=1，AB=，BC=，AA1=.

    （1）求证：A1B⊥B1C；

    （2）求二面角A1—B1C—B的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，为坐标原点，动点在圆外，过点作圆的切线，设切点为.

    （1）若点运动到处，求此时切线的方程；

    （2）求满足的点的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知直线y＝﹣2x+1与圆O：x2+y2＝r2（r＞0）交于M，N两点，且MN＝．

    （1）求M，N的坐标；

    （2）求过O，M，N三点的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面四个结论： ①数列可以看作是一个定义在正整数集(或它的有限子集{1，2，3……，n})上的函数；
    ②数列若用图象表示，从图象上看都是一群孤立的点；
    ③数列的项数是无限的；
    ④数列通项的表示式是唯一的．
    其中正确的是( )
    A.①②
    B.①②③
    C.②③
    D.①②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某校5个学生期末考试数学成绩和总分年级排名如下表：

    学生的编号

    1

    2

    3

    4

    5

    数学

    115

    112

    93

    125

    145

    年级排名

    250

    300

    450

    70

    10

    （1）通过大量事实证明发现，一个学生的数学成绩和总分年级排名具有很强的线性相关关系，在上述表格是正确的前提下，用表示数学成绩，用表示年级排名，求与的回归方程；（其中都取整数）

    （2）若在本次考试中，预计数学分数为120分的学生年级排名大概是多少？

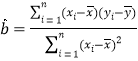    参考数据和公式：，其中，，其中

    查看答案和解析>>

    同步练习册答案