
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。曲线
为参数)。曲线![]() 的参数方程为
的参数方程为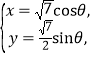 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点).
为坐标原点).
科目:高中数学 来源: 题型:
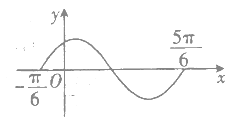
【题目】如图所示的是函数![]() (
(![]() ,
,![]() )在区间
)在区间![]() 上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移
上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移![]() (
(![]() )个单位长度后,所得到的图象关于直线
)个单位长度后,所得到的图象关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上一点,且
上一点,且![]() 到
到![]() 的焦点的距离为
的焦点的距离为![]() .
.
(1)若直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,证明:
为坐标原点,证明:![]() ;
;
(2)若![]() 是
是![]() 上一动点,点
上一动点,点![]() 不在直线
不在直线![]() :
:![]() 上,过
上,过![]() 作直线垂直于
作直线垂直于![]() 轴且交
轴且交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .试判断
.试判断![]() 与
与![]() 中是否有一个为定值?若是,请指出哪一个为定值,并加以证明;若不是,请说明理由.
中是否有一个为定值?若是,请指出哪一个为定值,并加以证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有以下四个命题:
有以下四个命题:
①对于任意的![]() ,都有
,都有![]() ; ②函数
; ②函数![]() 是偶函数;
是偶函数;
③若![]() 为一个非零有理数,则
为一个非零有理数,则![]() 对任意
对任意![]() 恒成立;
恒成立;
④在![]() 图象上存在三个点
图象上存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中正确命题的序号是__________.
为等边三角形.其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左右顶点分别为
)的左右顶点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 不经过点
不经过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过顶点.
过顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如列联表.
的概率分布如列联表.
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响求该企业在这两个月内共被消费者投诉![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
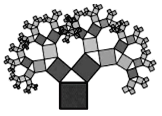
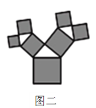
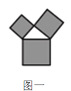
【题目】如图是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图一是第1代“勾股树”,重复图一的作法,得到图二为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第n代“勾股树”所有正方形的面积的和为( )
A. nB. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,AD=DC=AP=2,AB=1,点E为棱PC的中点.
,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com