
 中,底面
中,底面 为菱形,其中
为菱形,其中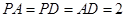 ,
, ,
, 为
为 的中点.
的中点.
 ;
; 平面
平面 ,且
,且 为
为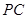 的中点,求四棱锥
的中点,求四棱锥 的体积.
的体积.科目:高中数学 来源:不详 题型:单选题
| A.①或② | B.②或③ | C.①或③ | D.只有② |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.直线m、n都平行于平面 ,则m∥n ,则m∥n |
B.设 是真二面角,若直线 是真二面角,若直线 ,则 ,则 |
C.设m、n是异面直线,若m∥平面 ,则n与 ,则n与 相交 相交 |
D.若直线m、n在平面 内的射影依次是一个点和一条直线,且 内的射影依次是一个点和一条直线,且 ,则 ,则 或 或 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A. aÌa, bÌa | B.aÌa, b//a | C. a^a, b^a | D.aÌa, b^a |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
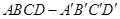 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题: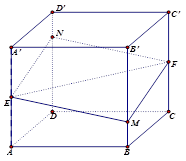

 平面
平面 ;
; 时,四边形
时,四边形 的面积最小;
的面积最小;  周长
周长 ,
, 是单调函数;
是单调函数; 的体积
的体积 为常函数;
为常函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: 上的点都在平面
上的点都在平面 内;
内; 上有些点不在平面
上有些点不在平面 内;
内; 内任意一条直线都不与直线
内任意一条直线都不与直线 平行.
平行.| A.3 | B.2 | C.1 | D.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.垂直和平行 | B.均为平行 | C.均为垂直 | D.不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com