
分析 (1)利用已知条件求出3a=2,代入g(x)=3ax-4x即可求解函数的解析式.
(2)化简方程,构造函数,利用数形结合求解实数b的取值范围.
解答 解:(1)∵函数f(x)=3x,且f(a+2)=18,∴3a+2=18⇒3a=2-----------(2分)
∵g(x)=3ax-4x=2x-4x,------------(4分)
(2)方程为2x-4x-b=0 令t=2x,x∈[-2,2],则$\frac{1}{4}≤t≤4$-----------(6分)
且方程为t-t2-b=0在有两个不同的解.
设y=t-t2=-(t-$\frac{1}{2}$)2+$\frac{1}{4}$,y=b 两函数图象在$[{\frac{1}{4},4}]$内有两个交点--------(8分)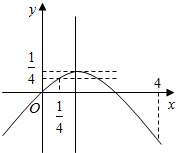
由图知$b∈[{\frac{3}{16},\frac{1}{4}})$时,方程有两不同解.--------(12分)
点评 本题考查函数的解析式的求法,函数的零点的求法,考查数形结合,考查计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0]∪[2,+∞) | B. | (-∞,0]∪(2,+∞) | C. | (-∞,0)∪[2,+∞) | D. | (-∞,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x3 | B. | f(x)=${x}^{-\frac{1}{2}}$ | C. | f(x)=-x | D. | f(x)=x+$\frac{3}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com