
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比到直线
的距离比到直线![]() 的距离小
的距离小![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)过点![]() 且倾斜角为
且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)设![]() 为曲线
为曲线![]() 上任意一点,点
上任意一点,点![]() ,是否存在垂直于
,是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 存在,其方程为
存在,其方程为![]() ,定值为
,定值为![]() .
.
【解析】
(1)利用抛物线的定义可求得曲线![]() 的方程,由题意可得直线
的方程,由题意可得直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,列出韦达定理,利用三角形的面积公式可求得
的方程联立,列出韦达定理,利用三角形的面积公式可求得![]() 的面积;
的面积;
(2)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,并设点
,并设点![]() ,求出以
,求出以![]() 为直径的圆的方程,将
为直径的圆的方程,将![]() 代入圆的方程,求出弦长的表达式,进而可求得
代入圆的方程,求出弦长的表达式,进而可求得![]() 的值,由此可求得直线
的值,由此可求得直线![]() 的方程.
的方程.
(1)依题意得,曲线![]() 上的点到点
上的点到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等,
的距离相等,
所以曲线![]() 的方程为:
的方程为:![]() .
.
过点![]() 且倾斜角为
且倾斜角为![]() 的直线方程为
的直线方程为![]() ,
,
设![]() ,
,![]() ,联立
,联立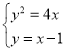 ,得
,得![]() ,
,
则![]() ,
,![]() ,则
,则![]() ;
;
(2)假设满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ,设点
,设点![]() ,
,
则以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
将直线![]() 代入,得
代入,得![]() ,
,
则![]() ,
,
设直线![]() 与以
与以![]() 为直径的圆的交点为
为直径的圆的交点为![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,
于是有![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 为定值.
为定值.
故满足条件的直线![]() 存在,其方程为
存在,其方程为![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() 相外切,且与直线
相外切,且与直线![]() 相切.
相切.
(1)记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求
,求![]() 的方程;
的方程;
(2)过点![]() 的两条直线
的两条直线![]() 与曲线
与曲线![]() 分别相交于点
分别相交于点![]() 和
和![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() .如果直线
.如果直线![]() 与
与![]() 的斜率之积等于1,求证:直线
的斜率之积等于1,求证:直线![]() 经过定点.
经过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,5,11,21,37,6l,95,则该数列的第8项为( )
A.99B.131C.139D.141
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等腰直角三角形ABC所在的平面与半圆弧AB所在的平面垂直,AC⊥AB,P是弧AB上一点,且∠PAB=30°.
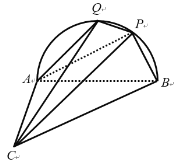
(1)证明:平面BCP⊥平面ACP;
(2)若Q是弧AP上异于AP的一个动点,当三棱锥C-APQ体积最大时,求二面角A-PQ-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
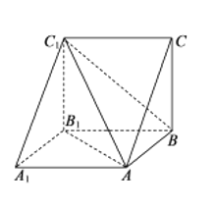
【题目】《九章算术》中记载:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱剖开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵![]() 中,
中,![]() 且有鳖臑C1-ABB1和鳖臑
且有鳖臑C1-ABB1和鳖臑![]() ,现将鳖臑
,现将鳖臑![]() 沿线BC1翻折,使点C与点B1重合,则鳖臑
沿线BC1翻折,使点C与点B1重合,则鳖臑![]() 经翻折后,与鳖臑
经翻折后,与鳖臑![]() 拼接成的几何体的外接球的表面积是______.
拼接成的几何体的外接球的表面积是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有![]() 的男生喜欢网络课程,有
的男生喜欢网络课程,有![]() 的女生不喜欢网络课程,且有
的女生不喜欢网络课程,且有![]() 的把握但没有
的把握但没有![]() 的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附: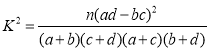 ,其中
,其中![]() .
.
|
|
|
|
|
k |
|
|
|
|
A.130B.190C.240D.250
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com