
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
分析 将一骰子向上抛掷两次,所得点数分别为m和n的基本事件个数有36个.函数y=mx2-4nx+1在[1,+∞)上为增函数包含的基本事件个数为9个,利用古典概型公式即可得到答案.
解答 解:函数y=mx2-4nx+1在[1,+∞)上为增函数,
等价于导数y′=2mx-4n≥0在[1,+∞)上恒成立.
而x≥$\frac{2n}{m}$在[1,+∞)上恒成立即$\frac{2n}{m}$≤1.
∵将一骰子向上抛掷两次,所得点数分别为m和n的基本事件个数为36个,
而满足$\frac{2n}{m}$≤1包含的(m,n)基本事件个数为9个,
故函数y=mx2-4nx+1在[1,+∞)上为增函数的概率是$\frac{9}{36}$=$\frac{1}{4}$,
故选:B.
点评 本题考查的是概率与函数的综合问题,利用古典概型的特点分别求出基本事件的总数及所求事件包含的基本事件的个数,利用导数解决函数的恒成立问题,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2018}{2019}$ | B. | $\frac{2017}{2018}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个都是篮球 | B. | 至少有1个是气排球 | ||
| C. | 3个都是气排球 | D. | 至少有1个是篮球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知椭圆 与双曲线
与双曲线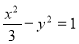 的离心率互为倒数,且直线
的离心率互为倒数,且直线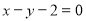 经过椭圆的右顶点.
经过椭圆的右顶点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设不过原点 的直线
的直线 与椭圆
与椭圆 交于
交于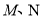 两点,且直线
两点,且直线 、
、 、
、 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△ 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
下列命题说法正确的是( )
A.命题“若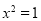 ,则
,则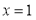 ”的否命题为:“若
”的否命题为:“若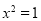 ,则
,则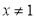 ”
”
B.“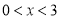 ”是“
”是“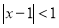 ”的必要不充分条件
”的必要不充分条件
C.命题“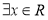 ,使得
,使得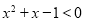 ”的否定是:“
”的否定是:“ ,均有
,均有 ”
”
D.命题“若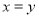 ,则
,则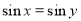 ”的逆命题为真命题
”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
无穷等比数列 中,“
中,“ ”是“数列
”是“数列 为递减数列”的( )
为递减数列”的( )
A.充分而不必要条件 B.充分必要条件
C.必要而不充分条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com