
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①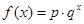 ;②
;②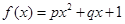 ;③
;③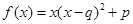 .(以上三式中、
.(以上三式中、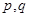 均为常数,且
均为常数,且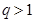 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(II)若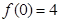 ,
,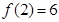 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是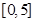 .其中
.其中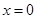 表示8月1日,
表示8月1日,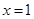 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)在(II)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:解答题
(本大题13分)设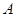 、
、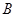 为函数
为函数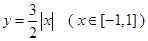 图象上不同的两个点,
图象上不同的两个点,
且 AB∥ 轴,又有定点
轴,又有定点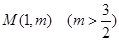 ,已知
,已知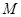 是线段
是线段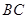 的中点.
的中点.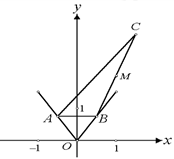
⑴ 设点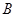 的横坐标为
的横坐标为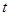 ,写出
,写出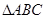 的面积
的面积 关于
关于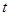 的函数
的函数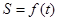 的表达式;
的表达式;
⑵ 求函数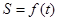 的最大值,并求此时点
的最大值,并求此时点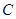 的坐标。
的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.(12分)飞机每飞行1小时的费用由两部分组成,固定部分为4900元,变动部分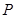 (元)与飞机飞行速度
(元)与飞机飞行速度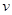 (千米∕小时)的函数关系式是
(千米∕小时)的函数关系式是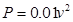 ,已知甲乙两地的距离为
,已知甲乙两地的距离为 (千米).
(千米).
(1)试写出飞机从甲地飞到乙地的总费用 (元)关于速度
(元)关于速度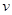 (千米∕小时)的函数关系式;
(千米∕小时)的函数关系式;
(2)当飞机飞行速度为多少时,所需费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
在一个月内分批购入每张价值为20元的书桌共36台,每批都购入x台(x是正整数), 且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
(1)求该月需用去的运费和保管费的总费用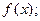
(2)能否恰当地安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com