
【题目】某校有一块圆心![]() ,半径为200米,圆心角为
,半径为200米,圆心角为![]() 的扇形绿地
的扇形绿地![]() ,半径
,半径![]() 的中点分别为
的中点分别为![]() ,
,![]() 为弧
为弧![]() 上的一点,设
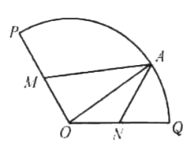
上的一点,设![]() ,如图所示,拟准备两套方案对该绿地再利用.
,如图所示,拟准备两套方案对该绿地再利用.
(1)方案一:将四边形绿地![]() 建成观赏鱼池,其面积记为
建成观赏鱼池,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
(2)方案二:将弧![]() 和线段
和线段![]() 围成区域建成活动场地,其面积记为
围成区域建成活动场地,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式;并求
的函数关系式;并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+3x+a
(1)当a=﹣2时,求不等式f(x)>2的解集
(2)若对任意的x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(Ⅱ)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.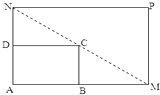
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(1)求f(0)的值和实数m的值;
(2)当m=1时,判断函数f(x)在(﹣1,1)上的单调性,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax2+2(a﹣3)x+1在区间[﹣2,+∞)上递减,则实数a的取值范围是( )
A.(﹣∞,﹣3]
B.[﹣3,0]
C.[﹣3,0)
D.[﹣2,0]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次水下考古活动中,某一潜水员需潜水50米到水底进行考古作业,其用氧量包含以下三个方面:
①下潜平均速度为![]() 米/分钟,每分钟的用氧量为
米/分钟,每分钟的用氧量为![]() 升;
升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.3升;
③返回水面时,平均速度为![]() 米/分钟,每分钟用氧量为0.32升;潜水员在此次考古活动中的总用氧量为
米/分钟,每分钟用氧量为0.32升;潜水员在此次考古活动中的总用氧量为![]() 升.
升.
(1)如果水底作业时间是10分钟,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,水底作业时间为20分钟,求总用氧量
,水底作业时间为20分钟,求总用氧量![]() 的取值范围;
的取值范围;
(3)若潜水员携带氧气13.5升,请问潜水员最多在水下多少分钟(结果取整数)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com