
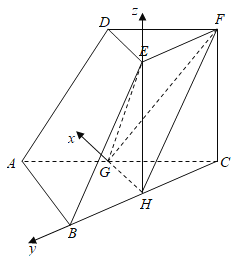
【题目】如图,在三棱台![]() 中,
中,![]() ,G,H分别为
,G,H分别为![]() ,
,![]() 上的点,平面
上的点,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
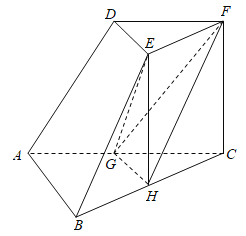
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明![]() ,
,![]() 得到
得到![]() 平面
平面![]() ,得到答案.
,得到答案.
(2)分别以![]() ,
,![]() ,
,![]() 所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系
所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系![]() ,计算平面
,计算平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为
![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
因为![]() ,所以
,所以![]() ,H为
,H为![]() 的中点.
的中点.
同理G为![]() 的中点,所以
的中点,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
又![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
分别以![]() ,
,![]() ,
,![]() 所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系
所在的直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,因为
,因为![]() ,
,![]()
则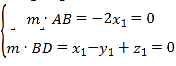 ,取
,取![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,因为
,因为![]() ,
,![]()
则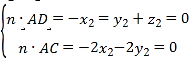 ,取
,取![]() ,得
,得![]() .
.
所以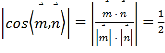 ,则二面角
,则二面角![]() 的大小为
的大小为![]()


科目:高中数学 来源: 题型:
【题目】算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如:在十位档拨上一颗上珠和一颗下珠,个位档拨上一颗上珠,则表示数字65.若在个、十、百、千位档中随机选择一档拨一颗上珠,再随机选择两个档位各拨一颗下珠,则所拨数字大于200的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于
(t为参数),直线l与曲线C分别交于![]() 两点.
两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才能:礼乐射御书数,某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种B.72种C.96种D.144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确命题的个数有( )
①![]() ,
,![]()
②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
③“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题
中至少有一个不小于2”的逆命题是真命题
④复数![]() ,则
,则![]() 的充分不必要条件是
的充分不必要条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 的底面是边长为2的正方形,平面
的底面是边长为2的正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
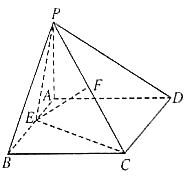
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 的中点,问边
的中点,问边![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,并求此时点
,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com