
【题目】命题p:f(x)=-x2+2ax+1-a在x∈[0,1]时的最大值不超过2,命题q:正数x,y满足x+2y=8,且![]() 恒成立. 若p∨(q)为假命题,求实数a的取值范围.
恒成立. 若p∨(q)为假命题,求实数a的取值范围.
【答案】实数a的取值范围是(-∞,-1).
【解析】分析:先求出关于![]() 为真时的a的取值范围,根据p∨(q)为假命题,得到p假q真,得到关于a的不等式组,解出即可.
为真时的a的取值范围,根据p∨(q)为假命题,得到p假q真,得到关于a的不等式组,解出即可.
详解:当a≤0时,f(x)max=f(0)=1-a≤2,解得-1≤a≤0;
当0<a<1时,f(x)max=f(a)=a2-a+1≤2,解得0<a<1;
当a≥1时,f(x)max=f(1)=a≤2,解得1≤a≤2.
所以使命题p为真的a的取值范围是[-1,2].
由x+2y=8,得![]() +
+![]() =1,又x,y都是正数,
=1,又x,y都是正数,
所以![]() +
+![]() =
=![]()
![]() =
=![]() +
+![]() ≥
≥![]() +2
+2![]() =1,当且仅当
=1,当且仅当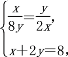 即
即![]() 时,等号成立,故
时,等号成立,故![]() min=1.
min=1.
因为a≤![]() +
+![]() 恒成立,所以a≤1,所以使命题q为真的a的取值范围是(-∞,1].
恒成立,所以a≤1,所以使命题q为真的a的取值范围是(-∞,1].
因为p∨(q)为假命题,所以p假q真,
所以![]() 则a<-1,
则a<-1,
故实数a的取值范围是(-∞,-1).


科目:高中数学 来源: 题型:
【题目】椭圆![]() 一个焦点为
一个焦点为![]() ,离心率
,离心率![]() .
.
(Ⅰ)求椭圆![]() 的方程式.
的方程式.
(Ⅱ)定点![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,求
上的动点,求![]() 的最大值;并求出取最大值时
的最大值;并求出取最大值时![]() 点的坐标求.
点的坐标求.
(Ⅲ)定直线![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,证明点
上的动点,证明点![]() 到
到![]() 的距离与到定直线
的距离与到定直线![]() 的距离的比值为常数,并求出此常数值.
的距离的比值为常数,并求出此常数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(1)求证:MN∥平面BDE;
(2)求二面角CEMN的正弦值;
(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名大学有男生14000人,女生10000人,该校体育学院想了解本校学生的运动状况,根据性别采取分层抽样的方法从全校学生中抽取120人,统计他们平均每天运动的时间,如下表:(平均每天运动的时间单位:小时,该校学生平均每天运动的时间范围是![]() ).
).
男生平均每天运动时间分布情况:

女生平均每天运动时间分布情况:

(1)请根据样本估算该校男生平均每天运动的时间(结果精确到0.1);
(2)若规定平均每天运动的时间不少于2小时的学生为“运动达人”,低于2小时的学生为“非运动达人”.
①请根据样本估算该校“运动达人”的数量;
②请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘运动达人’与性别有关?”
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘运动达人’与性别有关?”

参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(m) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=mxα的图象经过点A(2,2).
(1)试比较2ln f(3)与3ln f(2)的大小;
(2)定义在R上的函数g(x)满足g(-x)=g(x), g(4+x)=g(4-x),且当x∈[0,4]时,
 . 若关于x的不等式g 2(x)+ng(x)>0在[-200,200]上有且只有151个整数解,求实数n的取值范围。
. 若关于x的不等式g 2(x)+ng(x)>0在[-200,200]上有且只有151个整数解,求实数n的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是椭圆 ![]() 在第一象限上的动点,过点P引圆x2+y2=4的两条切线PA、PB,切点分别是A、B,直线AB与x轴、y轴分别交于点M、N,则△OMN面积的最小值为 .
在第一象限上的动点,过点P引圆x2+y2=4的两条切线PA、PB,切点分别是A、B,直线AB与x轴、y轴分别交于点M、N,则△OMN面积的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com