已知等比数列{an}的各项均为不等于1的正数,数列{bn}满足bn=lgan,b3=18,b6=12,则数列{bn}前n项和的最大值等于( )
A.126
B.130
C.132
D.134
【答案】
分析:由题意可知,lga
3=b
3,lga
6=b
6再由b
3,b
6,用a
1和q表示出a
3和b
6,进而求得q和a
1,根据{a
n}为正项等比数列推知{b
n}为等差数列,进而得出数列b
n的通项公式和前n项和,可知S
n的表达式为一元二次函数,根据其单调性进而求得S
n的最大值.
解答:解:由题意可知,lga
3=b
3,lga
6=b
6.
又∵b
3=18,b
6=12,则a
1q
2=10
18,a
1q
5=10
12,
∴q
3=10
-6.
即q=10
-2,∴a
1=10
22.
又∵{a
n}为正项等比数列,
∴{b
n}为等差数列,
且d=-2,b
1=22.
故b
n=22+(n-1)×(-2)=-2n+24.
∴S
n=22n+
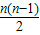
×(-2)
=-n
2+23n=
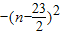
+

.又∵n∈N
*,故n=11或12时,(S
n)
max=132.
点评:本题主要考查了等比数列的性质.属基础题.

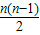 ×(-2)
×(-2)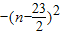 +
+ .又∵n∈N*,故n=11或12时,(Sn)max=132.
.又∵n∈N*,故n=11或12时,(Sn)max=132.

 名校课堂系列答案
名校课堂系列答案