
分析 判断函数f(x)=$\frac{1-{e}^{x}}{1+{e}^{x}}$的奇偶性,可判断(1);根据长方体对角线公式,可判断(2);根据复合函数单调性“同增异减”的原则,及对数函数的性质,求出a的范围,可判断(3);根据函数$f(x)=\frac{1}{x}$的图象和性质,可判断(4).
解答 解:(1)函数f(x)=$\frac{1-{e}^{x}}{1+{e}^{x}}$,满足f(-x)=-f(x),是奇函数,故错误;
(2)长方体的长宽高分别为a,b,c,对角线长为l,则l2=a2+b2+c2,故正确;
(3)在x∈[0,1]时,函数f(x)=loga(2-ax)是减函数,由t=2-ax为减函数,
故y=logat为增函数,故a>1,
又由2-ax>0,x∈[0,1]恒成立,故2-a>0,即a<2,
则实数a的取值范围是(1,2),故正确;
(4)函数$f(x)=\frac{1}{x}$在定义域内即是奇函数,但不是减函数,故错误.
故答案为:(2)(3)
点评 本题以命题的真假判断与应用为载体,考查了函数的单调性和奇偶性,长方体对角线公式等知识点,难度中档.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
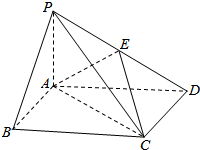 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
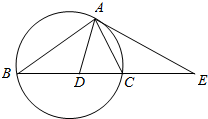 如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{{n}^{2}-n+2}{2}$ | B. | an=$\frac{{n}^{2}-n+1}{2}$ | C. | an=$\frac{2}{{n}^{2}-n+1}$ | D. | an=$\frac{2}{{n}^{2}-n+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com