
【题目】某网络购物平台每年11月11日举行“双十一”购物节,当天有多项优惠活动,深受广大消费者喜爱
(1)已知该网络购物平台近5年“双十”购物节当天成交额如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
成交额(百亿元) | 9 | 12 | 17 | 21 | 27 |
求成交额![]() (百亿元)与时间变量
(百亿元)与时间变量![]() (记2015年为
(记2015年为![]() ,2016年为
,2016年为![]() ,……依次类推)的线性回归方程,并预测2020年该平台“双十一”购物节当天的成交额(百亿元);
,……依次类推)的线性回归方程,并预测2020年该平台“双十一”购物节当天的成交额(百亿元);
(2)在2020年“双十一”购物节前,某同学的爸爸、妈妈计划在该网络购物平台.上分别参加![]() 、
、![]() 两店各一个订单的“秒杀”抢购,若该同学的爸爸、妈妈在
两店各一个订单的“秒杀”抢购,若该同学的爸爸、妈妈在![]() 、两店订单“秒杀”成功的概率分别为
、两店订单“秒杀”成功的概率分别为![]() 、
、![]() ,记该同学的爸爸和妈妈抢购到的订单总数量为
,记该同学的爸爸和妈妈抢购到的订单总数量为![]() .
.
(i)求![]() 的分布列及
的分布列及![]() ;
;
(ii)已知每个订单由![]() 件商品
件商品![]() 构成,记该同学的爸爸和妈妈抢购到的商品
构成,记该同学的爸爸和妈妈抢购到的商品![]() 总数量为
总数量为![]() ,假设
,假设 ,
, ,求
,求![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
【答案】(1)![]() ;30.7百亿元;(2)(i)分布列详见解析,
;30.7百亿元;(2)(i)分布列详见解析,![]() ;(ii)3.
;(ii)3.
【解析】
(1)计算![]() 、
、![]() ,求出系数
,求出系数![]() 和
和![]() ,写出线性回归方程,利用方程计算
,写出线性回归方程,利用方程计算![]() 时
时![]() 的值即可;
的值即可;
(2)![]() 由题意知随机变量
由题意知随机变量![]() 的可能取值,计算对应的概率值,写出分布列,求出数学期望值;
的可能取值,计算对应的概率值,写出分布列,求出数学期望值;
![]() 根据题意求出
根据题意求出![]() 的解析式,利用换元法和求导法计算
的解析式,利用换元法和求导法计算![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
解:(1)由已知可得:
![]() ,
,![]()
![]()
![]()
所以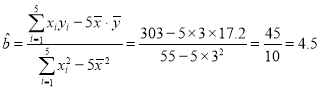
所以![]()
所以![]()
当![]() 时,
时,![]() (百亿元)
(百亿元)
所以估计2020年该平台“双十一”购物节当天的成交额为30.7(百亿元)
(2)(ⅰ)由题知,![]() 的可能取值为:0,1,2
的可能取值为:0,1,2
![]()
![]()
![]()
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]()
(ⅱ)因为![]()
所以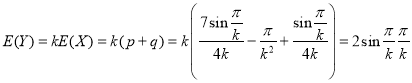
令![]() ,设
,设![]() ,则
,则![]()
因为![]() ,且
,且![]()
所以,当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减;
上单调递减;
所以,当![]() 即
即![]() 时,
时,![]() (百亿元)
(百亿元)
所以![]() 取最大值时
取最大值时![]() 的值为3
的值为3


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点.
的中点.

(1)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.

(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为2.
上的点到准线的最小距离为2.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 分别为弦
分别为弦![]() ,
,![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场春节期间推出一项优惠活动,活动规则如下:消费额每满300元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在区域Ⅰ返券60元;停在区域Ⅱ返券30元;停在区域Ⅲ不返券.例如:消费600元,可抽奖2次,所获得的返券金额是两次金额之和.
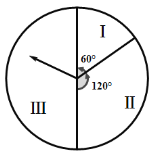
(Ⅰ)若某位顾客消费300元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费600元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率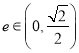 ,
,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点,![]() ,
,![]() 为椭圆的上、下顶点,且
为椭圆的上、下顶点,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,证明:在第一象限内存在定点
两点,证明:在第一象限内存在定点![]() ,使得当直线
,使得当直线![]() 与直线
与直线![]() 的斜率均存在时,其斜率之和是与
的斜率均存在时,其斜率之和是与![]() 无关的常数,并求出所有满足条件的定点
无关的常数,并求出所有满足条件的定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医院为筛查某种疾病,需要血检,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,需要检验![]() 次;
次;
方式二:混合检验,把每个人的血样分成两份,取![]() 个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这
个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这![]() 个人只作一次检验就够了;如果结果是阳性,那么再对这
个人只作一次检验就够了;如果结果是阳性,那么再对这![]() 个人的另一份血样逐份检验,此时这
个人的另一份血样逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.
次.
(1)假设有6份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验岀来的概率;
(2)假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是相互独立的,且每份样本是阳性结果的概率为![]() .现取其中
.现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019年高考数学的全国Ⅲ卷中,文科和理科的选做题题目完全相同,第22题考查选修4-4:极坐标和参数方程;第23题考查选修4-5:不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式,在测试结束后,该校数学组教师对该校全体高三学生的选做题得分情况进行了统计,得到两题得分的![]() 列联表如下(已知每名学生只做了一道题):
列联表如下(已知每名学生只做了一道题):
选做22题 | 选做23题 | 合计 | |
文科人数 | 50 | 60 | |
理科人数 | 40 | ||
总计 | 400 |
(1)完善![]() 列联表中的数据,判断能否有
列联表中的数据,判断能否有![]() 的把握认为“选做题的选择”与“文、理科的科类”有关;
的把握认为“选做题的选择”与“文、理科的科类”有关;
(2)经统计,第23题得分为0的学生中,理科生占理科总人数的![]() ,文科生占文科总人数的
,文科生占文科总人数的![]() ,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
附: ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com