
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在指出点
,若存在指出点![]() 的位置,若不存在请说明理由.
的位置,若不存在请说明理由.
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请全校
的值:先请全校![]() 名同学每人随机写下一个都小于
名同学每人随机写下一个都小于![]() 的正实数对
的正实数对![]() ;再统计两数能与
;再统计两数能与![]() 构成钝角三角形三边的数对
构成钝角三角形三边的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 估计
估计![]() 的值,那么可以估计
的值,那么可以估计![]() 的值约为( )
的值约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为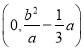 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存在
,是否存在![]() 使得
使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)
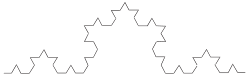
A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为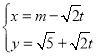 (其中
(其中![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 被
被![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求实数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() .底面
.底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
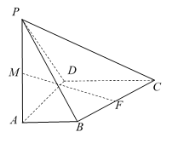
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E![]() 的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
的左、右焦点分别为F1,F2,P是双曲线E上的一点,且|PF2|=2|PF1|,若直线PF2与双曲线E的渐近线交于点M,且M为PF2的中点,则双曲线E的渐近线方程为( )
A.y=±![]() B.y=±
B.y=±![]() C.y=±2xD.y=±3x
C.y=±2xD.y=±3x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com