
【题目】我国的烟花名目繁多,花色品种繁杂.其中“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,通过研究,发现该型烟花爆裂时距地面的高度h(单位:米)与时间t(单位:秒)存在函数关系,并得到相关数据如下表:
时间t |
| 2 | 4 |
高度h | 10 | 25 | 17 |
( I)根据上表数据,从下列函数中,选取一个函数描述该型烟花爆裂时距地面的高度h与时间t的变化关系:y1=kt+b,y2=at2+bt+c,y3=abt , 确定此函数解析式,并简单说明理由;
( II)利用你选取的函数,判断烟花爆裂的最佳时刻,并求出此时烟花距地面的高度.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆C: ![]() =1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
=1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
(1)证明:b2=ad;
(2)若M的坐标为( ![]() ,1),求椭圆C的方程.
,1),求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x(x∈[﹣1,2])的值域为集合A,g(x)=ax+2(x∈[﹣1,2])的值域为集合B.若AB,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩. 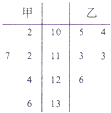
(1)从甲班的样本中有放回的随机抽取2个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名学生的成绩,记获优秀成绩的总人数为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图为某市2017年2月28天的日空气质量指数折线图.
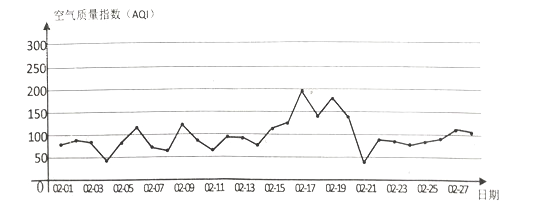
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:

(1)请根据所给的折线图补全下方的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
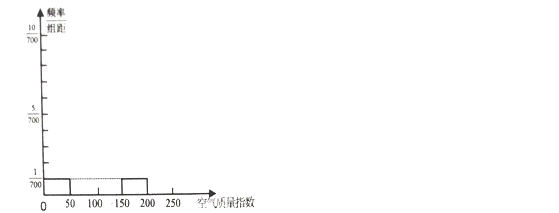
(2)研究人员发现,空气质量指数测评中![]() 与燃烧排放的
与燃烧排放的![]() 两个项目存在线性相关关系,以
两个项目存在线性相关关系,以![]() 为单位,下表给出
为单位,下表给出![]() 与
与![]() 的相关数据:
的相关数据:

求![]() 关于
关于![]() 的回归方程,并估计当
的回归方程,并估计当![]() 排放量是
排放量是![]() 时,
时, ![]() 的值.
的值.
(用最小二乘法求回归方程的系数是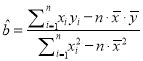 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x+1|+|x﹣1|.
(1)求f(x)≤x+2的解集;
(2)若不等式f(x)≤log2(a2﹣4a+12)对任意实数a恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数是同一函数的是( )
① ![]() 与
与 ![]() ;
;
②f(x)=|x|与 ![]() ;
;
③f(x)=x0与g(x)=1;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①②
B.①③
C.②④
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com