
【题目】如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF//AE,AB=AE=2.
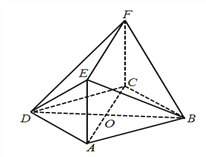
(1)求证:BD⊥平面ACFE;
(2)当直线FO与平面BDE所成的角为45°时,求二面角B﹣EF﹣D的余弦值.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】给出下列函数:①f(x)=(![]() )x;②f(x)=x2;③f(x)=x3;④f(x)=
)x;②f(x)=x2;③f(x)=x3;④f(x)=![]() ;⑤f(x)=log2x.其中满足条件f(
;⑤f(x)=log2x.其中满足条件f(![]() )>
)>![]() (0<x1<x2)的函数的个数是( )
(0<x1<x2)的函数的个数是( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() , 若椭圆上一点
, 若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 是点
是点![]() 在
在![]() 轴上的垂足,延长
轴上的垂足,延长![]() 交椭圆
交椭圆![]() 于
于![]() ,求证:
,求证: ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
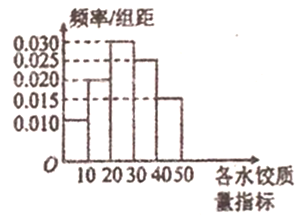
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市初三毕业生参加中考要进行体育测试,某实验中学初三(8)班的一次体育测试成绩的茎叶图和频率分布直方图都受到不同程度的涂黑,但可见部分如图,据此解答如下问题.
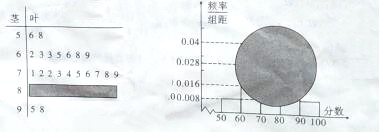
(Ⅰ)求全班人数及中位数,并重新画出频率直方图;
(Ⅱ)若要从分数在![]() 之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在
之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com