
����Ŀ��ij��������ˮ�����������£�ԭʼ��ˮ���Ⱦ���Aϵͳ����,���������ˮ��A��ˮ���ﵽ����������ƴ�꣩�ĸ���Ϊ![]() .��������,��ȷ�ϴ����ֱ���ŷţ����������������Bϵͳ������ֱ���ŷ�.
.��������,��ȷ�ϴ����ֱ���ŷţ����������������Bϵͳ������ֱ���ŷ�.
ij������![]() ����ˮ����A��ˮ��,�ֱ�ȡ�������. �����ˮ�������ʱ,�ȿ����������,Ҳ���Խ����ɸ����������һ����.���������ֻҪ�����������,���������Ļ������ز����.��������������,������и�������������������飻������������,��ԭˮ�ص���ˮֱ���ŷ�.
����ˮ����A��ˮ��,�ֱ�ȡ�������. �����ˮ�������ʱ,�ȿ����������,Ҳ���Խ����ɸ����������һ����.���������ֻҪ�����������,���������Ļ������ز����.��������������,������и�������������������飻������������,��ԭˮ�ص���ˮֱ���ŷ�.
�����������ַ���,
����һ��������飻
��������ƽ���ֳ����黯�飻
��������������������һ����,ʣ�µ�һ���������飻
�����ģ�����һ����.
�������������ֵԽС,����Խ���š�.
���� ��![]() ,��
,��![]() ��A��ˮ������ϻ�����������ĸ��ʣ�
��A��ˮ������ϻ�����������ĸ��ʣ�
���� ��![]() ,����
,����![]() ��A��ˮ������Ҫ����,���ʣ�����һ,��,�����ĸ���š���
��A��ˮ������Ҫ����,���ʣ�����һ,��,�����ĸ���š���
���� �������������ȡ������ġ������š�,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡�����![]() ;��II��������;��III��������.
;��II��������;��III��������.
���������������������������������¼��ظ������ĸ���Ϊ��������¼����ʳ˻�����������¼��ĸ��ʺ�Ϊ![]() ���ɵý�������ֱ�������ַ�����Ӧ�ֲ��У���һ��������Ե�����ֵ���Ƚ�����ֵ��С�����ŷ��������ֱ��������ֵ������������С��ϵ��������
���ɵý�������ֱ�������ַ�����Ӧ�ֲ��У���һ��������Ե�����ֵ���Ƚ�����ֵ��С�����ŷ��������ֱ��������ֵ������������С��ϵ��������![]() �IJ���ʽ�����
�IJ���ʽ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������������û���������ĸ�����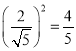 �� 2��
�� 2��
���Ը��ݶ����¼�ԭ���������ĸ���Ϊ![]() ��
��
��II������һ�������⣬������Ϊ![]() ��
��
���������ɣ�I��֪��ÿ�����������ļ��ʱ��������������Ϊ![]() ������Ϊ
������Ϊ![]() ����������������Ϊ
����������������Ϊ![]() ������Ϊ
������Ϊ![]() �� �ʷ������ļ�����
�� �ʷ������ļ�����![]() ��
�� ![]() ����ȡ
����ȡ![]() ��
�� ![]() ��
�� ![]() �����ʷֲ������£�
�����ʷֲ������£�
|
|
|
|
|
|
|
|
����÷�����������Ϊ![]() ��
��
�����ģ�����һ���⣬�Ǽ�����Ϊ![]() ��
�� ![]() ��ȡ
��ȡ![]() ��
�� ![]() �����ʷֲ������£�
�����ʷֲ������£�
|
|
|
|
|
|
����÷����ĵ�����Ϊ![]() ��
��
�ȽϿɵ�![]() ����ѡ������š���
����ѡ������š���
��III���⣺���������軯�����![]() ��
�� ![]() ��ȡ
��ȡ![]() ��
�� ![]() ��
��
|
|
|
|
|
|
![]() ��
��
�����ģ��軯�����![]() ��
�� ![]() ��ȡ
��ȡ![]() ��
�� ![]() ��
��
|
|
|
|
|
|
![]() ��
��
�������![]()
![]() ��
��
�ʵ�![]() ʱ���������ȷ����ĸ���������
ʱ���������ȷ����ĸ���������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�����ABCD��A1B1C1D1�У�AB=2 ![]() ��AD=2
��AD=2 ![]() ��AA1=2��BC��A1C1���ɵĽ�=�� AA1��BC1���ɵĽ�=�ȣ�
��AA1=2��BC��A1C1���ɵĽ�=�� AA1��BC1���ɵĽ�=�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�����Σ�PA��ƽ��ABCD��PA=AD=2����BAD=60�㣮 
��1����֤��ƽ��PBD��ƽ��PAC��
��2�����A��ƽ��PBD�ľ��룻
��3��������A��PB��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��![]() �ĵ�����.
�ĵ�����.
��1����![]() ��
��![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() ��
��![]() ��
��![]() ʱȡ����Сֵ����
ʱȡ����Сֵ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���ڣ�1���������£���![]() ʱ��
ʱ�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ķ�����Ϊ����1��1��������g��x��=f�� ![]() ��+f��x��1���Ķ�����Ϊ�� ��
��+f��x��1���Ķ�����Ϊ�� ��
A.����2��0��
B.����2��2��
C.��0��2��
D.���� ![]() ��0��
��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ���溯����
���溯����
��1����ʵ��a��ֵ��
��2���ö���֤������f��x����R�ϵĵ����ԣ�
��3�����������x��R������ʽf��x2��x��+f��2x2��k����0���������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������![]() ��,����
��,����![]() ������
������![]() ,
, ![]() ,
, ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е�,
���е�, ![]() ,
, ![]() ,
, ![]() ��
��

����֤����ֱ��![]() ��ƽ��
��ƽ��![]() ��
��
����������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��= ![]() ��x��R������f��x������f����x��=��f��x����
��x��R������f��x������f����x��=��f��x����
��1����ʵ��a��ֵ��
��2��֤��f��x����R�ϵĵ��������������巨����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() �Ƕ����ڣ���1��1���ϵ��溯������f��1��=1��
�Ƕ����ڣ���1��1���ϵ��溯������f��1��=1��
��1������f��x���Ľ���ʽ��
��2���жϲ�֤��f��x���ڣ���1��1���ϵĵ����ԣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com