
【题目】已知函数![]() 的导函数
的导函数![]() 是偶函数,若方程
是偶函数,若方程![]() 在区间
在区间![]() (其中
(其中![]() 为自然对数的底)上有两个不相等的实数根,则实数
为自然对数的底)上有两个不相等的实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
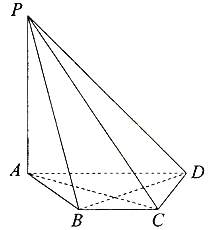
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)若两人分别从甲、乙两个盒子中各摸出一球,规定:两人谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),这样规定公平吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() 上的两个动点,点
上的两个动点,点![]() 在第一象限,点
在第一象限,点![]() 在第四象限,
在第四象限,![]() 分别过点
分别过点![]() 且与抛物线
且与抛物线![]() 相切,
相切,![]() 为
为![]() 的交点.
的交点.
(Ⅰ)若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,求证动点
,求证动点![]() 在一条定直线上,并求此直线方程;
在一条定直线上,并求此直线方程;
(Ⅱ)设![]() 为直线
为直线![]() 与直线
与直线![]() 的交点,求
的交点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省第九届少数民族传统体育运动会于2018年10月16日至20日在湘西龙山举行.运动会期间,湖南省14个市州和17个民族县市区组成的31个代表团2631人参加,来自土家、苗、瑶、侗、白、维吾尔、壮、回、汉等22个民族的1991名运动员分别参加陀螺、射弩、秋千、高脚、板鞋、蹴球、键球、押加、民族健身操及表演项目比赛,是湖南省历届民族运动会规模最大、规格最高、参赛人数最多的一次.对本次运动会中320名志愿者的年龄抽样调查统计后得到样本频率分布直方图(如图),但是年龄组为![]() 的数据不慎丢失,请完成下面的解答.
的数据不慎丢失,请完成下面的解答.
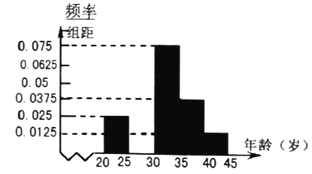
(1)将频率分布直方图补充完整;
(2)估计本次省民运会中志愿者年龄的众数和中位数(结果保留两位小数);
(3)已知样本容量为16,现在需要从样本中30岁以下的志愿者中抽取2名志愿者谈对本次运动会的感想,求被抽中的志愿者中恰有一名志愿者年龄不小于25岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批苹果中随机抽取50个,其质量(单位:![]() )的频数分布表如下:
)的频数分布表如下:
分组 |
|
|
|
|
频数 | 5 | 10 | 20 | 15 |
用分层随机抽样的方法从质量在![]() 和
和![]() 内的苹果中共抽取4个,再从抽取的4个苹果中任取2个,则有1个苹果的质量在
内的苹果中共抽取4个,再从抽取的4个苹果中任取2个,则有1个苹果的质量在![]() 内的概率为( )
内的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部![]() 是矩形,其中
是矩形,其中![]() 米,
米,![]() 米;上部
米;上部![]() 是等边三角形,固定点
是等边三角形,固定点![]() 为
为![]() 的中点.
的中点.![]() 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),![]() 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和![]() 平行的伸缩横杆.
平行的伸缩横杆.
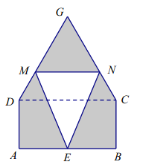
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() 米,试将
米,试将![]() 的面积
的面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数;
的函数;
(2)求![]() 的面积
的面积![]() (平方米)的最大值.
(平方米)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com