练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线m：2x﹣y﹣3＝0与直线n：x+y﹣3＝0的交点为P，若直线l过点P，且点A（1，3）和B（3，2）到l的距离相等，求l的方程

    【答案】x+2y﹣4＝0或x＝2．

    【解析】

    联立直线的方程，求得点的坐标.将的斜率分成不存在和存在两种情况进行分类讨论，结合到直线的距离相等，求得直线的方程.

    直线m：2x﹣y﹣3＝0与直线n：x+y﹣3＝0的交点为P，

    解方程组，得，∴P（2，1），

    直线l过点P，且点A（1，3）和B（3，2）到l的距离相等，

    当直线l的斜率不存在时，直线l的方程为x＝2，成立；

    当直线l的斜率k存在时，设直线l的方程为y﹣1＝k（x﹣2），即kx﹣y﹣2k+1＝0，

    ∵点A（1，3）和B（3，2）到l的距离相等，

    ∴，解得k，

    ∴l的方程为，即x+2y﹣4＝0．

    综上，l的方程为x+2y﹣4＝0或x＝2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱中，，侧面底面，是的中点，，.

    （Ⅰ）求证：为直角三角形；

    （Ⅱ）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校研究性学习小组对该校高二学生视力情况进行调查，学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到如下数据：

    年级名次

    是否近视

    1～50

    951～1000

    近视

    41

    32

    不近视

    9

    18

    （1）根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系？

    （2）在（1）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50名的学生人数为，求的分布列和数学期望.

    0.10

    0.05

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    附：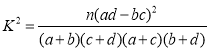

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的部分图象如图所示：

    （I）求的解析式及对称中心坐标；

    （Ⅱ）将的图象向右平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数的图象,求函数在上的单调区间及最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，底面ABCD为菱形，，点O为AD的中点，且.

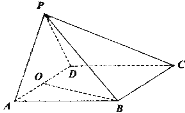
    （1）求证：平面PAD；

    （2）若，求平面PBC与平面PAD所成二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，角A，B，C的对边分别为a，b，c，.

    （1）求角C；

    （2）设D为边AC上一点，AD＝BD，若BC＝2，的面积为3，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数满足，且在上无最小值，则______，函数的单调减区间为______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分13分） 已知椭圆经过点，离心率为，过点的直线与椭圆交于不同的两点．

    （1）求椭圆的方程；

    （2）求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求下列椭圆的标准方程：

    （1）已知椭圆长轴是短轴的倍，并且过点；

    （2）已知椭圆经过两点、.

    查看答案和解析>>

    同步练习册答案