
【题目】已知恒等式(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n .
(1)求a1+a2+a3+…+a2n和a2+2a3+22a4+…+22n﹣2a2n的值;
(2)当n≥6时,求证: ![]() a2+2A
a2+2A ![]() a3+…+22n﹣2
a3+…+22n﹣2 ![]() a2n<49n﹣2 .
a2n<49n﹣2 .
【答案】
(1)解:令x=0,则a0=1.
令x=1,则a0+a1+a2+…+a2n=3n,∴a1+a2+…+a2n=3n﹣1.
∵(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n.
∴两边对x求导可得:n(1+x+x2)n﹣1=a1+2a2x+…+2na2nx2n﹣1.
令x=0,则n=a1,
由(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n.
令x=2,则 ![]() ×7n=
×7n= ![]() +
+ ![]() +a2+2a3+…+22n﹣2a2n.
+a2+2a3+…+22n﹣2a2n.
∴a2+2a3+…+22n﹣2a2n= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
(2)证明:∵(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n.
∴两边对x求导可得:n(1+x+x2)n﹣1(1+2x)=a1+2a2x+…+2na2nx2n﹣1,
再一次求导可得:n[(n﹣1)(1+2x)2+2](1+x+x2)n﹣2=2a2+3×2a3x+…+2n(2n﹣1)a2nx2n﹣2,
![]() =k(k﹣1),
=k(k﹣1),
令x=2可得: ![]() a2+2A
a2+2A ![]() a3+…+22n﹣2
a3+…+22n﹣2 ![]() a2n=n[25(n﹣1)+2]×7n﹣2,
a2n=n[25(n﹣1)+2]×7n﹣2,
n≥6时,n[25(n﹣1)+2]<7n﹣2,
∴ ![]() a2+2A
a2+2A ![]() a3+…+22n﹣2
a3+…+22n﹣2 ![]() a2n=n[25(n﹣1)+2]×7n﹣2<49n﹣2.
a2n=n[25(n﹣1)+2]×7n﹣2<49n﹣2.
【解析】(1)令x=0,则a0=1.令x=1,a0+a1+a2+…+a2n=3n , 可得a1+a2+…+a2n . 由(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n . 两边对x求导可得:n(1+x+x2)n﹣1=a1+2a2x+…+2na2nx2n﹣1 . 令x=0,可得n=a1 , 由(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n . 令x=2,可得 ![]() ×7n=
×7n= ![]() +
+ ![]() +a2+2a3+…+22n﹣2a2n . 即可得出.(2)(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n . 由(1)可得:n(1+x+x2)n﹣1(1+2x)=a1+2a2x+…+2na2nx2n﹣1 , 两边对x求导可得:n[(n﹣1)(1+2x)2+2](1+x+x2)n﹣2=2a2+3×2a3x+…+2n(2n﹣1)a2nx2n﹣2 , 令x=2可得:
+a2+2a3+…+22n﹣2a2n . 即可得出.(2)(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n . 由(1)可得:n(1+x+x2)n﹣1(1+2x)=a1+2a2x+…+2na2nx2n﹣1 , 两边对x求导可得:n[(n﹣1)(1+2x)2+2](1+x+x2)n﹣2=2a2+3×2a3x+…+2n(2n﹣1)a2nx2n﹣2 , 令x=2可得: ![]() a2+2A
a2+2A ![]() a3+…+22n﹣2
a3+…+22n﹣2 ![]() a2n=n[25(n﹣1)+2]×7n﹣2 , n≥6时,n[25(n﹣1)+2]<7n﹣2 , 即可证明.
a2n=n[25(n﹣1)+2]×7n﹣2 , n≥6时,n[25(n﹣1)+2]<7n﹣2 , 即可证明.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() )的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
)的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2)
=1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2) 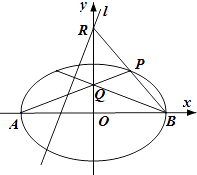
(1)求椭圆C的标准方程;
(2)求证: ![]() 为定值;
为定值;
(3)求证:过点R且与直线QB垂直的直线经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对一年级的甲、乙两个班进行“数学学前教育”对“小学数学成绩优秀”影响的试验,其中甲班为试验班(实施了数学学前教育),乙班为对比班(和甲班一样进行常规教学,但没有实施数学学前教育),在期末测试后得到如下数据:
优秀人数 | 非优秀人数 | 总计 | |
甲班 | 30 | 20 | 50 |
乙班 | 25 | 25 | 50 |
总计 | 55 | 45 | 100 |
能否在犯错误的概率不超过0.01的前提下,认为进行“数学学前教育”对“小学数学成绩优秀”有积极作用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线x+y+
,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线x+y+![]() =0相切.A,B分别是椭圆C的左、右顶点,直线l过B点且与x轴垂直.
=0相切.A,B分别是椭圆C的左、右顶点,直线l过B点且与x轴垂直.
(1)求椭圆C的标准方程;
(2)设G是椭圆C上异于A,B的任意一点,过点G作GH⊥x轴于点H,延长HG到点Q使得|HG|=|GQ|,连接AQ并延长交直线l于点M,N为线段MB的中点,判断直线QN与以AB为直径的圆O的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q. 
(1)若直线l的斜率为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏. 
(1)若当∠OBC= ![]() 时,sin∠BCO=
时,sin∠BCO= ![]() ,求此时a的值;
,求此时a的值;
(2)设y=CA2+CB2 , 且CA2+CB2≤232.
(i)试将y表示为a的函数,并求出a的取值范围;
(ii)若同时要求市民在水池边缘任意一点C处观赏喷泉时,观赏角度∠ACB的最大值不小于 ![]() ,试求A,B两处喷泉间距离的最小值.
,试求A,B两处喷泉间距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com