
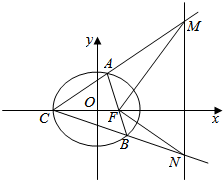
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F与抛物线y2=4x的焦点重合,D(1,$\frac{3}{2}$)是椭圆上一点,椭圆左顶点为C,过F的直线与椭圆交于A、B两点,直线CA、CB与直线1:x=4交于点M、N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F与抛物线y2=4x的焦点重合,D(1,$\frac{3}{2}$)是椭圆上一点,椭圆左顶点为C,过F的直线与椭圆交于A、B两点,直线CA、CB与直线1:x=4交于点M、N.分析 (I)一方面通过抛物线y2=4x的焦点F(1,0)可知a2-b2=1,另一方面通过将点D(1,$\frac{3}{2}$)代入椭圆方程可知$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,联立计算可知a2=4、b2=3,进而计算可得结论;
(Ⅱ)通过(I)可知C(-2,0),显然直线AB的斜率不为零,分直线AB的斜率不存在与存在两种情况讨论,①当直线AB的斜率不存在时可知直线AB方程为x=1,从而A(1,$\frac{3}{2}$)、B(1,-$\frac{3}{2}$),计算即得结论;②当直线AB的斜率存在时,设直线AB方程为:y=k(x-1)、A(x1,y1)、B(x2,y2),进而在直线CA:y=$\frac{{y}_{1}}{{x}_{1}+2}$(x+2)、直线CB:y=$\frac{{y}_{2}}{{x}_{2}+2}$(x+2)令x=4可知M(4,6•$\frac{{y}_{1}}{{x}_{1}+2}$)、N(4,6•$\frac{{y}_{2}}{{x}_{2}+2}$),通过联立直线AB与椭圆方程、利用韦达定理可知x1+x2、x1x2,利用向量数量积的坐标运算可知$\overrightarrow{FM}$•$\overrightarrow{FN}$=0.
解答 解:(I)∵抛物线y2=4x的焦点F(1,0),
∴a2-b2=1,①
又∵D(1,$\frac{3}{2}$)是椭圆上一点,
∴$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,②
联立①②可知:a2=4,b2=3,
∴所求椭圆方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1;
(Ⅱ)由(I)可知C(-2,0),显然直线AB的斜率不为零,
①当直线AB的斜率不存在时,即直线AB方程为:x=1,
易知A(1,$\frac{3}{2}$),B(1,-$\frac{3}{2}$),
∴直线CA:y=$\frac{\frac{3}{2}-0}{1+2}$(x+2),直线CB:y=$\frac{-\frac{3}{2}-0}{1+2}$(x+2),
即直线CA:y=$\frac{1}{2}$(x+2),直线CB:y=-$\frac{1}{2}$(x+2),
分别在上述两个方程中令x=4可知:M(4,3)、N(4,-3),
∴$\overrightarrow{FM}$•$\overrightarrow{FN}$=(4-1,3-0)•(4-1,-3-0)
=(3,3)•(3,-3)
=0;
②当直线AB的斜率存在时,设直线AB方程为:y=k(x-1),
设A(x1,y1),B(x2,y2),则yi=k(xi-1)、$\frac{{{x}_{i}}^{2}}{4}+\frac{{{y}_{i}}^{2}}{3}=1$(其中i=1、2),
∴直线CA:y=$\frac{{y}_{1}-0}{{x}_{1}+2}$(x+2),直线CB:y=$\frac{{y}_{2}-0}{{x}_{2}+2}$(x+2),
即直线CA:y=$\frac{{y}_{1}}{{x}_{1}+2}$(x+2),直线CB:y=$\frac{{y}_{2}}{{x}_{2}+2}$(x+2),
分别在上述两个方程中令x=4可知:M(4,6•$\frac{{y}_{1}}{{x}_{1}+2}$)、N(4,6•$\frac{{y}_{2}}{{x}_{2}+2}$),
联立$\left\{\begin{array}{l}{y=kx-k}\\{3{x}^{2}+4{y}^{2}-12=0}\end{array}\right.$,消去y整理得:(3+4k2)x2-8k2x+4k2-12=0,
∴x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
∴$\overrightarrow{FM}$•$\overrightarrow{FN}$=(4-1,6•$\frac{{y}_{1}}{{x}_{1}+2}$-0)•(4-1,6•$\frac{{y}_{2}}{{x}_{2}+2}$-0)
=9+36•$\frac{{y}_{1}}{{x}_{1}+2}$•$\frac{{y}_{2}}{{x}_{2}+2}$
=9+36•$\frac{{k}^{2}[{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1]}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$
=9+36k2•$\frac{\frac{4{k}^{2}-12}{3+4{k}^{2}}-\frac{8{k}^{2}}{3+4{k}^{2}}+1}{\frac{4{k}^{2}-12}{3+4{k}^{2}}+2•\frac{8{k}^{2}}{3+4{k}^{2}}+4}$
=9+36k2•$\frac{4{k}^{2}-12-8{k}^{2}+3+4{k}^{2}}{4{k}^{2}-12+16{k}^{2}+12+16{k}^{2}}$
=9+36k2•$\frac{-9}{36{k}^{2}}$
=0;
综上所述,$\overrightarrow{FM}$•$\overrightarrow{FN}$=0.
点评 本题考查椭圆的简单性质,考查分类讨论的思想,注意解题方法的积累,属于难题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | |a|=|b| | B. | a<0且a=-b | C. | a>0且a≠b | D. | a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
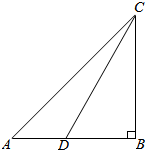 如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.
如图,一人在某山脚B的正西方向A处测得山顶C的仰角为45°,再向正东方向行进(3-$\sqrt{3}$)百米后到D,测得山顶C在D的北偏东30°,则该山BC的高度为( )百米.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com