
设二面角的![]() -AB-
-AB-![]() 大小为α,AC
大小为α,AC![]() 平面
平面![]() ,∠CAB=β,AC与平面
,∠CAB=β,AC与平面![]() 成θ角,则α,β,θ之间的关系是
成θ角,则α,β,θ之间的关系是
A.sinα+sinθ=sinβ
B.sinαsinβ=sinθ
C.sinαsinθ=sinβ
D.sinβsinθ=sinα
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届浙江省杭州市高二上学期期末考试理科数学试卷 题型:解答题
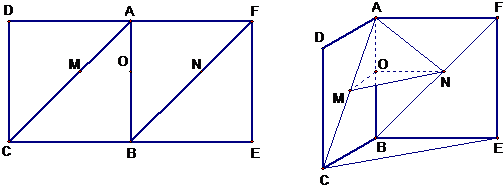
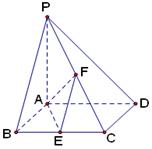
如图,已知四棱锥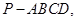 底面
底面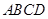 为菱形,
为菱形,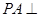 平面
平面 ,
,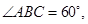
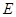 、
、 分别是
分别是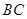 、
、 的中点.
的中点.
(1)证明:
(2)设AB=2, 若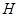 为线段
为线段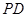 上的动点,
上的动点,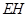 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为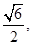 求二面角
求二面角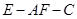 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省金华市义乌二中高二(上)期中数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:四川省南充高中08-09学年高二下学期第四次月考(理) 题型:解答题
如图甲,已知PA垂直于⊙O所在平面,AB是⊙O的直径,点C为圆周上异于A、B的一点.
(1)若一个 面体中有
面体中有 个面是直角三角形,则称这个
个面是直角三角形,则称这个 面体的直度为
面体的直度为 .那么四面体
.那么四面体 的直度为多少?说明理由;
的直度为多少?说明理由;
 (2)在四面体
(2)在四面体 中,
中, ,设
,设 .若动点
.若动点 在四面体
在四面体 表面上运动,并且总保持
表面上运动,并且总保持 .设
.设 为动点
为动点 的轨迹围成的封闭图形的面积关于角
的轨迹围成的封闭图形的面积关于角 的函数,求
的函数,求 取最大值时,二面角
取最大值时,二面角 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com