
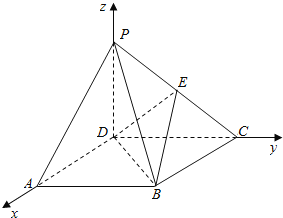
【题目】如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.

(Ⅰ)证明PA//平面BDE;
(Ⅱ)求二面角B—DE—C的平面角的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】
(Ⅰ)以D为坐标原点,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,利用向量法能证明PA∥平面BDE;(Ⅱ)由已知求出平面BDE的一个法向量和平面DEC的一个法向量,利用向量法能求出二面角B﹣DE﹣C的余弦值;(Ⅲ)由已知得PB⊥DE,假设棱PB上存在点F,使PB⊥平面DEF,设![]() ,(0<λ∠1),由此利用向量法能求出在棱PB上存在点F,PF=
,(0<λ∠1),由此利用向量法能求出在棱PB上存在点F,PF=![]() ,使得PB⊥平面DEF.
,使得PB⊥平面DEF.
(Ⅰ)证明:以D为坐标原点,
分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),B(2,2,0),
![]() =(2,0,﹣2),
=(2,0,﹣2),![]() =(0,1,1),
=(0,1,1),![]() ,
,
设![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
则由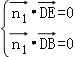 ,得
,得![]() ,
,
取y=﹣1,得![]() .
.
∵![]() =2﹣2=0,∴
=2﹣2=0,∴![]() ,
,
又PA不包含于平面BDE,PA∥平面BDE;
(Ⅱ)由(Ⅰ)知![]() =(1,﹣1,1)是平面BDE的一个法向量,
=(1,﹣1,1)是平面BDE的一个法向量,
又![]() =
=![]() =(2,0,0)是平面DEC的一个法向量.
=(2,0,0)是平面DEC的一个法向量.
设二面角B﹣DE﹣C的平面角为θ,
∴cosθ=cos<![]() ,
,![]() >=
>=![]() .
.
故二面角B﹣DE﹣C的余弦值为![]() .
.
(Ⅲ)∵![]() =(2,2,﹣2),
=(2,2,﹣2),![]() =(0,1,1),
=(0,1,1),
∴![]() =0,∴PB⊥DE,
=0,∴PB⊥DE,
假设棱PB上存在点F,使PB⊥平面DEF,设![]() ,(0<λ∠1),
,(0<λ∠1),
则![]() =(2λ,2λ,﹣2λ),
=(2λ,2λ,﹣2λ),![]() =
=![]() =(2λ,2λ,2﹣2λ),
=(2λ,2λ,2﹣2λ),
由![]() =0,得4λ2+4λ2﹣2λ(2﹣2λ)=0,
=0,得4λ2+4λ2﹣2λ(2﹣2λ)=0,
∴![]() ∈(0,1),此时PF=
∈(0,1),此时PF=![]() ,
,
即在棱PB上存在点F,PF=![]() ,使得PB⊥平面DEF.
,使得PB⊥平面DEF.


科目:高中数学 来源: 题型:
【题目】(2018·湖北襄阳模拟)已知椭圆C:![]() (a>b>0)的焦点为F1,F2,P是椭圆C上一点,若PF1⊥PF2,|F1F2|=2
(a>b>0)的焦点为F1,F2,P是椭圆C上一点,若PF1⊥PF2,|F1F2|=2![]() ,△PF1F2的面积为1.
,△PF1F2的面积为1.
(1)求椭圆C的方程;
(2)如果椭圆C上总存在关于直线y=x+m对称的两点A,B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:

(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内温度,四周墙上装有如图所示的通风设施,该设施的下部是等边三角形ABC,其中AB=2米,上部是半圆,点E为AB的中点.△EMN是通风窗,(其余部分不通风)MN是可以沿设施的边框上下滑动且保持与AB平行的伸缩杆(MN和AB不重合).
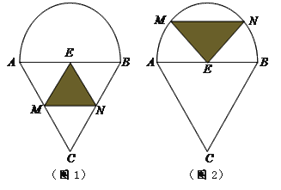
(1)设MN与C之间的距离为x米,试将△EMN的面积S表示成![]() 的函数
的函数![]() ;
;
(2)当MN与C之间的距离为多少时,△EMN面积最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间y(分) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为![]() =
= ,
,![]() =
=![]() -
-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}中,bn>0(n∈N*),且b1+b2+b3=15,又a1+b1、a2+b2、a3+b3成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{an·bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com