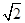【答案】
分析:法一:可以先把向量

,
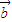
,
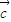
放入平面直角坐标系,则
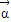
=(x
1,0),

=(

,y
1),再用
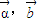
的坐标表示

的坐标,利用
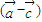
•
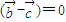
,可转化为含y
1的式子,再看y
1等于多少时,m-n有最小值即可.
法二:我们分别令
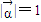
,

=

,

=

,根据由已知中,向量

,

,

满足

,
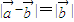
,

•

.可判断出A,B,C三点的位置关系,及m-n的几何意义,进而得到答案.
解答:解:法一:把

放入平面直角坐标系,使

起点与坐标原点重合,方向与x轴正方向一致,则

=(1,0)
设
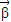
=(x
1,y
1),∵

,∴x1=

,∴
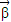
=(

,y
1)
设
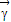
=(x,y),则

=(1-x,-y),
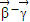
=(

-x,y
1-y)
∵(
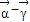
)•(
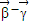
)=0.∴(1-x)(

-x)-y(y
1-y)=0
化简得,x
2+y
2-

x-y
1y+

=0,也即
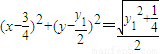
点(x,y)可表示圆心在(

,
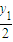
),半径为

的圆上的点,

=

,∴

最大m=
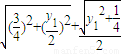
,最小值n=

.
∴m-n=

-(

)=
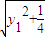
当y
12=0时,m-n有最小值为

,
法二:解:∵
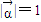
,
∴令

=

则A必在单位圆上,
又∵又向量

满足
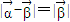
,
∴令

=

则点B必在线段OA的中垂线上,
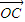
=

.
又∵

故C点在以线段AB为直径的圆M上,任取一点C,记
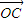
=
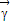
.
故m-n就是圆M的直径|AB|
显然,当点B在线段OA的中点时,(m-n)取最小值

即(m-n)
min=

故选B.
点评:本题考查的知识点是两向量的和与差的模的最值,及向量加减法的几何意义,其中根据已知条件,判断出A,B,C三点的位置关系,及m-n的几何意义,是解答本题的关键.

 ,
,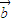 ,
,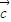 满足
满足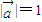 ,
, ,
, •
•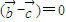 .若对每一确定的
.若对每一确定的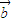 ,
, 的最大值和最小值分别为m,n,则对任意
的最大值和最小值分别为m,n,则对任意 ,m-n的最小值是( )
,m-n的最小值是( )


 ,
,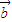 ,
,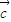 放入平面直角坐标系,则
放入平面直角坐标系,则 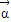 =(x1,0),
=(x1,0), =(
=(  ,y1),再用
,y1),再用 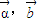 的坐标表示
的坐标表示  的坐标,利用
的坐标,利用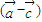 •
•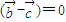 ,可转化为含y1的式子,再看y1等于多少时,m-n有最小值即可.
,可转化为含y1的式子,再看y1等于多少时,m-n有最小值即可.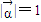 ,
, =
= ,
, =
= ,根据由已知中,向量
,根据由已知中,向量 ,
, ,
, 满足
满足 ,
,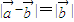 ,
, •
• .可判断出A,B,C三点的位置关系,及m-n的几何意义,进而得到答案.
.可判断出A,B,C三点的位置关系,及m-n的几何意义,进而得到答案. 放入平面直角坐标系,使
放入平面直角坐标系,使  起点与坐标原点重合,方向与x轴正方向一致,则
起点与坐标原点重合,方向与x轴正方向一致,则  =(1,0)
=(1,0)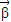 =(x1,y1),∵
=(x1,y1),∵ ,∴x1=
,∴x1= ,∴
,∴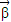 =(
=(  ,y1)
,y1)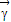 =(x,y),则
=(x,y),则  =(1-x,-y),
=(1-x,-y),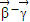 =(
=(  -x,y1-y)
-x,y1-y)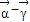 )•(
)•( 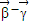 )=0.∴(1-x)(
)=0.∴(1-x)(  -x)-y(y1-y)=0
-x)-y(y1-y)=0 x-y1y+
x-y1y+ =0,也即
=0,也即 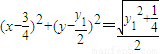
 ,
,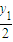 ),半径为
),半径为  的圆上的点,
的圆上的点, =
= ,∴
,∴ 最大m=
最大m=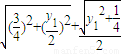 ,最小值n=
,最小值n= .
. -(
-(  )=
)=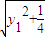
 ,
,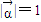 ,
, =
= 则A必在单位圆上,
则A必在单位圆上, 满足
满足 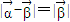 ,
, =
= 则点B必在线段OA的中垂线上,
则点B必在线段OA的中垂线上,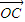 =
= .
.
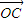 =
=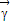 .
.



 、
、 、
、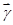 满足
满足 ,
,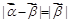 ,
,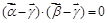 .若对每一确定的
.若对每一确定的 ,
,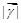 的最大值和最小值分别为
的最大值和最小值分别为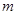 、
、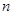 ,则对任意
,则对任意 ,
,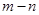 的最小值是 ( )
的最小值是 ( )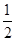 B.1 C.2 D.
B.1 C.2 D.