
分析 运用等差数列和等比数列的求和公式求得An,Bn,运用数列的求和方法:分组求和可得Sn,再由数列的极限:$\underset{lim}{n→∞}$qn=0,即可得到d,q的方程,解方程可得所求.
解答 解:由题意可得前n项的和为An=n+$\frac{1}{2}$n(n-1)d,
Bn=$\frac{1-{q}^{n}}{1-q}$,Sn=B1+B2+…+Bn=($\frac{1}{1-q}$-$\frac{q}{1-q}$)+($\frac{1}{1-q}$-$\frac{{q}^{2}}{1-q}$)+…+($\frac{1}{1-q}$-$\frac{{q}^{n}}{1-q}$)
=$\frac{n}{1-q}$-($\frac{q}{1-q}$+$\frac{{q}^{2}}{1-q}$+…+$\frac{{q}^{n}}{1-q}$)=$\frac{n}{1-q}$-$\frac{1}{1-q}$•$\frac{q(1-{q}^{n})}{1-q}$,
若$\underset{lim}{n→∞}$($\frac{{A}_{n}}{n}$-Sn)=1,即有$\underset{lim}{n→∞}$[1+$\frac{1}{2}$(n-1)d-$\frac{n}{1-q}$+$\frac{1}{1-q}$•$\frac{q(1-{q}^{n})}{1-q}$]=1,
由$\underset{lim}{n→∞}$qn=0,可得1-$\frac{1}{2}$d+$\frac{q}{(1-q)^{2}}$=1,且$\frac{1}{2}$d-$\frac{1}{1-q}$=0,
解方程可得d=4,q=$\frac{1}{2}$.
点评 本题考查数列的极限的求法,运用$\underset{lim}{n→∞}$qn=0,同时考查等差数列和等比数列的求和公式的运用,以及数列的求和方法:分组求和,属于中档题.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
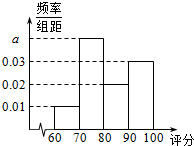 某生产车间为了检测其加工的零件的质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测指标评分大于60分的零件为合格零件,指标评分不超过40分的零件将直接被淘汰,指标评分在(40,60]内的零件可能被修复也可能被淘汰.现质检员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示,
某生产车间为了检测其加工的零件的质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测指标评分大于60分的零件为合格零件,指标评分不超过40分的零件将直接被淘汰,指标评分在(40,60]内的零件可能被修复也可能被淘汰.现质检员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示,| 零件检测指标评分所在区间 | (40,50] | (50,60] |
| 每个零件个体被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,+∞) | B. | (0,+∞) | C. | (0,2)∪[$\frac{5}{2}$,+∞) | D. | (-∞,2)∪[$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2a | B. | 2a-1 | C. | ($\frac{1}{2}$)a-1 | D. | 1-($\frac{1}{2}$)a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com