
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( ) 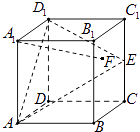
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}
≤t≤2}
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
【答案】D
【解析】解:设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
分别取B1B、B1C1的中点M、N,连接AM、MN、AN,

则∵A1M∥D1E,A1M平面D1AE,D1E平面D1AE,
∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线
∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F平面A1MN,即点F是线段MN上上的动点.
设直线A1F与平面BCC1B1所成角为θ
运动点F并加以观察,可得
当F与M(或N)重合时,A1F与平面BCC1B1所成角等于∠A1MB1,此时所成角θ达到最小值,满足tanθ= ![]() =2;
=2;
当F与MN中点重合时,A1F与平面BCC1B1所成角达到最大值,满足tanθ= ![]() =2
=2 ![]()
∴A1F与平面BCC1B1所成角的正切取值范围为[2,2 ![]() ]
]
故选:D
【考点精析】掌握空间角的异面直线所成的角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1. 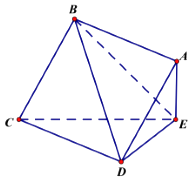
(1)求证:AB∥平面CDE;
(2)求证:DE⊥平面ABE;
(3)求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥V﹣ABCD中,底面ABCD是边长2为的正方形,其他四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 
(1)求正四棱锥V﹣ABCD的体积.
(2)求二面角V﹣BC﹣A的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a1=1,又a1 , a2 , a5成公比不为1的等比数列. (Ⅰ)求数列{an}的公差;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,﹣3),B(2,﹣1)和直线l:4x+3y﹣2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]()
![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为正数的等差数列,a1a2=3,a2a3=15.
(1)求数列{an}的通项公式;
(2)设bn=(an+1)2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com