
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(1)求f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最值.
【答案】
(1)解:设x∈[0,1],则﹣x∈[﹣1,0].∴f(x)= ![]() =4x﹣2x
=4x﹣2x
又∵f(﹣x)=﹣f(x)=﹣(4x﹣2x)∴f(x)=2x﹣4x.
所以,f(x)在[0,1]上的解析式为f(x)=2x﹣4x
(2)解:当x∈[0,1],f(x)=2x﹣4x=﹣(2x)2+2x,
∴设t=2x(t>0),则y=﹣t2+t∵x∈[0,1],∴t∈[1,2]
当t=1时x=0,f(x)max=0;当t=2时x=1,f(x)min=﹣2
【解析】(1)设x∈[0,1],则﹣x∈[﹣1,0],利用条件结合奇函数的定义求f(x)在[0,1]上的解析式;(2)设t=2x(t>0),则y=﹣t2+t,利用二次函数的性质求f(x)在[0,1]上的最值.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及下面一些统计量的值.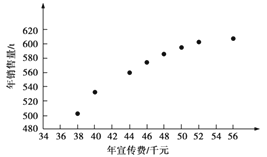
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中 ![]() ,
, ![]() .
.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最下二乘估计分别为 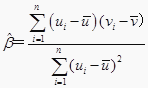 ,
, ![]() .
.
(1)根据散点图判断,y=a+bx与 ![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
①年宣传费x=49时,年销售量及年利润的预报值时多少?
②年宣传费x为何值时,年利润的预报值最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Rt△ABC的斜边BC在平面α内,则△ABC的两条直角边在平面α内的正射影与斜边组成的图形只能是( )
A.一条线段
B.一个锐角三角形或一条线段
C.一个钝角三角形或一条线段
D.一条线段或一个钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校毕业典礼由6个节目组成,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起,则该校毕业典礼节目演出顺序的编排方案共有
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点, ![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 分别与直线
分别与直线![]() 和直线
和直线![]() 交于
交于![]() 两点.
两点.
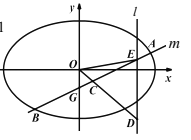
(1)求直线![]() 的斜率和直线
的斜率和直线![]() 的斜率之积;
的斜率之积;
(2)分别记![]() 和
和![]() 的面积为
的面积为![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点A、B、C及平面内一点P满足 ![]() +
+ ![]() =
= ![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A.P在△ABC的内部
B.P在△ABC的边AB上
C.P在AB边所在直线上
D.P在△ABC的外部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1= ![]() ,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点.
,AB=1,AD=2,E为BC的中点,点M为棱AA1的中点. 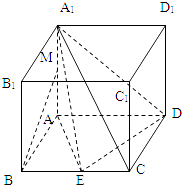
(1)证明:DE⊥平面A1AE;
(2)证明:BM∥平面A1ED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的x∈[﹣1,2],都有x2﹣2x+a≤0(a为常数),则a的取值范围是( )
A.(﹣∞,﹣3]
B.(﹣∞,0]
C.[1,+∞)
D.(﹣∞,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com