
【题目】函数![]() (
(![]() ,
,![]() 是自然对数的底数,
是自然对数的底数,![]() )存在唯一的零点,则实数
)存在唯一的零点,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
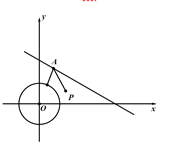
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马再回到军营,怎样走才能使总路程最短?在如图所示的直角坐标系![]() 中,设军营所在平面区域为
中,设军营所在平面区域为![]() ,河岸线所在直线方程为
,河岸线所在直线方程为![]() .假定将军从点
.假定将军从点![]() 处出发,只要到达军营所在区域即回到军营,则将军可以选择最短路程为_____________.
处出发,只要到达军营所在区域即回到军营,则将军可以选择最短路程为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
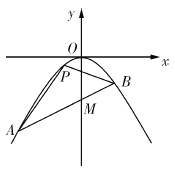
【题目】如图,拋物线的顶点![]() 在坐标原点,焦点在
在坐标原点,焦点在![]() 轴负半轴上,过点
轴负半轴上,过点![]() 作直线
作直线![]() 与拋物线相交于
与拋物线相交于![]() 两点,且满足
两点,且满足![]() .
.
(1)求直线![]() 和拋物线的方程;
和拋物线的方程;
(2)当拋物线上一动点![]() 从点
从点![]() 运动到点
运动到点![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,且
,且![]() .
.
(1)求![]() 的通项公式.
的通项公式.
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 成立的最小的正整数
成立的最小的正整数![]() .
.
(3)设![]() .若数列
.若数列![]() 单调递增.
单调递增.
①求![]() 的取值范围.
的取值范围.
②若![]() 是符合条件的最小正整数,那么
是符合条件的最小正整数,那么![]() 中是否存在三项
中是否存在三项![]() 依次成等差数列?若存在,给出
依次成等差数列?若存在,给出![]() 的值.若不存在,说明理由.
的值.若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题为真命题的序号是__________.
①“若![]() 则
则![]() ”是真命题.
”是真命题.
②“若![]() 则
则![]() ”的逆命题是真命题.
”的逆命题是真命题.
③![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
④“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 互相垂直”的充要条件.
互相垂直”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 恰好是椭圆
恰好是椭圆![]() 的右焦点.
的右焦点.
(1)求实数![]() 的值及抛物线
的值及抛物线![]() 的准线方程;
的准线方程;
(2)过点![]() 任作两条互相垂直的直线分别交抛物线
任作两条互相垂直的直线分别交抛物线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() 点,求两条弦的弦长之和
点,求两条弦的弦长之和![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=![]() CD=1,PD=
CD=1,PD=![]() .
.

(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PE与平面PBC所成角的正弦值.
(3)在PC上是否存在一点Q,使得平面QAD与平面PBC所成锐二面角的大小为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com