
分析 (1)求出导函数,曲线曲线的斜率以及切点坐标,然后求解切线方程,代入$({3,\frac{9}{2}})$求出a即可.
(2)利用导函数的单调性以及函数的极值,列出不等式求解即可.
(3)当x>0时,f(x)<0恒成立,则$lnx-ax-\frac{1}{2}{x^3}<0$,即$a>\frac{lnx}{x}-\frac{1}{2}{x^2}$对x>0恒成立.
设$g(x)=\frac{lnx}{x}-\frac{1}{2}{x^2}({x>0})$,求出导函数$g′(x)=\frac{{1-lnx-{x^3}}}{x^2}$,设h(x)=1-lnx-x3(x>0),再求解函数的导数,判断函数的单调性以及最值,求出$g{(x)_{max}}=g(1)=-\frac{1}{2}$,然后求解a的取值范围.
解答 解:(1)∵$f′(x)=\frac{1}{x}-a-\frac{3}{2}{x^2}$,
∴$f′(1)=-a-\frac{1}{2}$,∵$f(1)=-a-\frac{1}{2}$,
∴曲线y=f(x)在点(1,f(1))处的切线方程为$y+a+\frac{1}{2}=-({a+\frac{1}{2}})({x-1})$,
代入$({3,\frac{9}{2}})$得a+5=-2a-1⇒a=-2.
(2)∵$f′(x)=\frac{1}{x}-a-\frac{3}{2}{x^2}$为(0,+∞)上的减函数,
f(x)在(1,2)上存在极值,
∴$\left\{{\begin{array}{l}{f′(1)>0}\\{f′(2)<0}\end{array}}\right.⇒a∈({-\frac{11}{2},-\frac{1}{2}})$.
(3)当x>0时,f(x)<0恒成立,则$lnx-ax-\frac{1}{2}{x^3}<0$,
即$a>\frac{lnx}{x}-\frac{1}{2}{x^2}$对x>0恒成立.
设$g(x)=\frac{lnx}{x}-\frac{1}{2}{x^2}({x>0})$,$g′(x)=\frac{{1-lnx-{x^3}}}{x^2}$,
设h(x)=1-lnx-x3(x>0),$h′(x)=-\frac{1}{x}-3{x^2}<0$,
∴h(x)在(0,+∞)上递减,
又h(1)=0,则当0<x<1时,h(x)>0,g′(x)>0;
当x>1时,h(x)<0,g′(x)<0.
∴$g{(x)_{max}}=g(1)=-\frac{1}{2}$,∴$a>-\frac{1}{2}$,
即a的取值范围为$({-\frac{1}{2},+∞})$.
点评 本题考查函数的导数的应用,切线方程,极值以及函数的最值,构造法二次导数的应用,考查分析问题解决问题的能力.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 回归分析 | B. | 独立性检验分析 | C. | 残差分析 | D. | 散点图分析 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4029 | B. | 4030 | C. | 4031 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{π}{4},\frac{π}{2}})$ | B. | $[{\frac{π}{4},\frac{3π}{4}}]$ | C. | $[{\frac{π}{4},π})$ | D. | $[{0,\frac{π}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
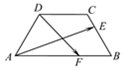 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )| A. | λ∈($\frac{1}{8}$,$\frac{1}{4}$) | B. | λ∈($\frac{1}{4}$,$\frac{3}{8}$) | C. | λ∈($\frac{3}{8}$,$\frac{1}{2}$) | D. | λ∈($\frac{1}{2}$,$\frac{5}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com