
如果有穷数列 (
(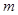 为正整数)满足
为正整数)满足 .即
.即 ,我们称其为“对称数列“例如,数列
,我们称其为“对称数列“例如,数列 ,
, ,
, ,
, ,
, 与数列
与数列 ,
, ,
, ,
, ,
, ,
, 都是“对称数列”.设
都是“对称数列”.设 是项数为
是项数为 的“对称数列”,并使得
的“对称数列”,并使得 ,
, ,
, ,
, ,…,
,…, 依次为该数列中连续的前
依次为该数列中连续的前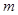 项,则数列
项,则数列 的前
的前 项和
项和 可以是
可以是
⑴ ⑵
⑵ (3)
(3)
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
解析考点:数列的应用.
专题:新定义.
分析:由题意由于新定义了对称数列,且已知数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,故数列bn的前2010项利用等比数列的前n项和定义直接可求(1)(2)的正确与否;对于(3),先从等比数列的求和公式求出任意2m项的和在利用减法的到需要的前201008项的和,即可判断.
解答:解:因为数列bn是项数为不超过2m(m>1,m∈N*)的“对称数列”,并使得1,2,22,…,2m-1依次为该数列中前连续的m项,故数列bn的前2010项可以是:①1,2,22,23…,21005,21005,…,22,1.
所以前2010项和S2010=2×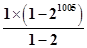 =2(21005-1),所以(1)错(2)对;
=2(21005-1),所以(1)错(2)对;
对于 (3)1,2,22,…2m-2,2m-1,2 m-2,…,2,1,1,2,…2m-2,2m-1,2 m-2,…,2,1…m-1=2n+1,利用等比数列的求和公式可得:S2010=2m+1-22m-2010-1,故(3)正确.
故为C
点评:本题以新定义对称数列为切入点,运用的知识都是数列的基本知识:等差数列的通项及求和公式,等比数列的通项及求和公式,还体现了分类讨论在解题中的应用.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
(07年上海卷文)(14分)如果有穷数列![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() ,
,![]() ,…,
,…,![]() ,即
,即![]() (
(![]() ),我们称其为“对称数列”.
),我们称其为“对称数列”.
例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)设![]() 是7项的“对称数列”,其中
是7项的“对称数列”,其中![]() 是等差数列,且
是等差数列,且![]() ,
,![]() .依次写出
.依次写出![]() 的每一项;
的每一项;
(2)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,求
的等比数列,求![]() 各项的和
各项的和![]() ;
;
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.求
的等差数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年扬州中学) 如果有穷数列![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() ,
,![]() ,…,
,…,![]() ,即
,即![]() (
(![]() ),我们称其为“对称数列”.例如,由组合数组成的数列
),我们称其为“对称数列”.例如,由组合数组成的数列![]() 就是“对称数列”.
就是“对称数列”.
(1)设![]() 是项数为7的“对称数列”,其中
是项数为7的“对称数列”,其中![]() 是等差数列,且
是等差数列,且![]() ,
,![]() .依次写出
.依次写出![]() 的每一项;
的每一项;
(2)设![]() 是项数为
是项数为![]() (正整数
(正整数![]() )的“对称数列”,其中
)的“对称数列”,其中![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.记
的等差数列.记![]() 各项的和为
各项的和为![]() .当
.当![]() 为何值时,
为何值时,![]() 取得最大值?并求出
取得最大值?并求出![]() 的最大值;
的最大值;
(3)对于确定的正整数![]() ,写出所有项数不超过
,写出所有项数不超过![]() 的“对称数列”,使得
的“对称数列”,使得![]() 依次是该数列中连续的项;当
依次是该数列中连续的项;当![]()
![]() 时,求其中一个“对称数列”前
时,求其中一个“对称数列”前![]() 项的和
项的和![]()
查看答案和解析>>
科目:高中数学 来源:2010年湖南省衡阳八中高二上学期期中考试数学试卷 题型:解答题
(本小题满分10分)如果有穷数列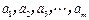 (
(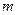 为正整数)满足条件
为正整数)满足条件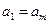 ,
,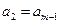 ,…,
,…,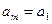 ,即
,即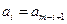 (
(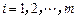 ),我们称其为“对称数列”.
),我们称其为“对称数列”.
例如,数列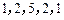 与数列
与数列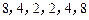 都是“对称数列”.
都是“对称数列”.
(1)设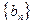 是7项的“对称数列”,其中
是7项的“对称数列”,其中 是等差数列,且
是等差数列,且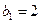 ,
,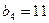 .依次写出
.依次写出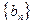 的每一项;
的每一项;
(2)设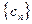 是
是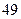 项的“对称数列”,其中
项的“对称数列”,其中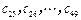 是首项为
是首项为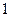 ,公比为
,公比为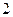 的等比数列,求
的等比数列,求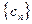 各项的和
各项的和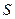 ;
;
(3)设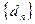 是
是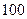 项的“对称数列”,其中
项的“对称数列”,其中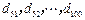 是首项为
是首项为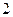 ,公差为
,公差为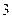 的等差数列.求
的等差数列.求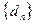 前
前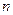 项的和
项的和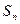
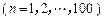 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三下学期期初考试数学理卷 题型:选择题
如果有穷数列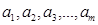 (
(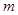 为正整数)满足
为正整数)满足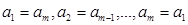 .即
.即 ,我们称其为“对称数列“例如,数列
,我们称其为“对称数列“例如,数列 ,
,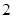 ,
,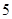 ,
,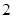 ,
, 与数列
与数列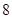 ,
,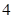 ,
,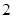 ,
,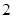 ,
,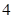 ,
,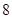 都是“对称数列”.设
都是“对称数列”.设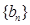 是项数为
是项数为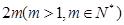 的“对称数列”,并使得
的“对称数列”,并使得 ,
,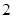 ,
, ,
,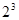 ,…,
,…,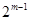 依次为该数列中连续的前
依次为该数列中连续的前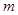 项,则数列
项,则数列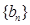 的前
的前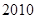 项和
项和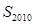 可以是
可以是
⑴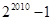 ⑵
⑵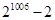 (3)
(3)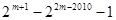
其中正确命题的个数为 ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com