
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 对于选项①,②值,代入相应的公式求即可,对于选项③,④值域代入相应的公式时需要分类讨论,故要用到条件语句来描述其算法
解答 解:对于①输入一个数x,求它的相反数,代入y=-x求即可;
对于②,求面积为6的正方形的周长,代入C=4$\sqrt{a}$求即可;
对于③,求三个数a,b,c中的最大数,必须先进行大小比较,要用条件语句;
对于④,求函数f(x)=$\left\{\begin{array}{l}{x-1,x≥0}\\{x+2,x<0}\end{array}\right.$的函数值,必须对所给的x进行条件判断,也要用条件语句.
其中不需要用条件语句来描述其算法的有2个.
故选:B
点评 本题考查算法适宜用条件结构的问题,是在解决时需要讨论的问题.属于基础题.


科目:高中数学 来源: 题型:解答题
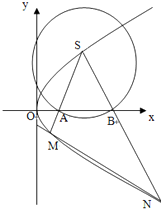 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{7}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$或-$\frac{4}{9}$ | D. | -$\frac{2}{9}$或$\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com