
【题目】已知函数f(x)=sin(x+θ)+ ![]() cos(x+θ),
cos(x+θ), ![]() ,且函数f(x)是偶函数,则θ的值为 .
,且函数f(x)是偶函数,则θ的值为 .
【答案】![]()
【解析】解:f(x)=sin(x+θ)+ ![]() cos(x+θ) =2(
cos(x+θ) =2( ![]() )
)
= ![]()
当 ![]() (k∈Z)
(k∈Z)
即: ![]()
由于: ![]()
所以:当k=0时,θ= ![]()
所以答案是: ![]()
【考点精析】掌握函数奇偶性的性质和函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】空间四边形ABCD中,AB=CD且异面直线AB与CD所成的角为30°,E,F为BC和AD的中点,则异面直线EF和AB所成的角为( )
A.15°
B.30°
C.45°或75°
D.15°或75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x﹣6y+12=0,点A(3,5).
(1)求过点A的圆的切线方程;
(2)O点是坐标原点,连接OA,OC,求△AOC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.若 ![]() 与
与 ![]() 互为负向量,则
互为负向量,则 ![]() +
+ ![]() =0
=0
B.若 ![]()
![]() =0,则
=0,则 ![]() =
= ![]() 或
或 ![]() =
= ![]()
C.若 ![]() ,
, ![]() 都是单位向量,则
都是单位向量,则 ![]()
![]() =1
=1
D.若k为实数且k ![]() =
= ![]() ,则k=0或
,则k=0或 ![]() =
= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养正中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),校总务处计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设![]() (单位:弧度),用
(单位:弧度),用![]() 表示弓形BCD的面积
表示弓形BCD的面积![]()
(2)如果该校总务处邀请你规划这块土地。如何设计![]() 的大小才能使总利润最大?并求出该最大值
的大小才能使总利润最大?并求出该最大值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( ) 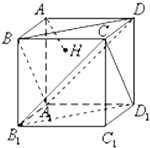
A.点H是△A1BD的垂心
B.AH的延长线经过点C1
C.AH垂直平面CB1D1
D.直线AH和BB1所成角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中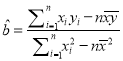 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时f(x)=2x﹣x2 ,
(1)求f(x)的表达式;
(2)设0<a<b,当x∈[a,b]时,f(x)的值域为 ![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com