
| A�� | g��x�����溯�� | B�� | g��x����ͼ�����ֱ��x=-$\frac{��}{4}$�Գ� | ||
| C�� | g��x����[$\frac{��}{4}$��$\frac{��}{2}$]�ϵ������� | D�� | ��x��[$\frac{��}{6}$��$\frac{2��}{3}$]ʱ��g��x����ֵ����[-2��1] |
���� �������Һ�������������æص�ֵ���ɵ�f��x���Ľ���ʽ�������ú���y=Asin����x+�գ���ͼ��任���ɣ����g��x���Ľ���ʽ�����������Һ�����ͼ��ĶԳ��ԣ����Һ����ĵ����ԡ��������ֵ�ó����ۣ�
��� �⣺����f��x��=2sin����x+$\frac{��}{6}$����ͼ����x�ύ��ĺ����꣬
���ι���һ������Ϊ$\frac{��}{2}$�ĵȲ����У�
��$\frac{T}{2}$=$\frac{1}{2}•\frac{2��}{��}$=$\frac{��}{2}$�����=2��f��x��=2sin��2x+$\frac{��}{6}$����
�Ѻ���f��x����ͼ����x������ƽ��$\frac{��}{6}$����λ��
�õ�����g��x��=2sin[2��x+$\frac{��}{6}$��+$\frac{��}{6}$]=2sin��2x+$\frac{��}{2}$��=2cos2x��ͼ��
��g��x����ż���������ų�A��
��x=-$\frac{��}{4}$ʱ��g��x��=0����g��x����ͼ����ֱ��x=-$\frac{��}{4}$�Գƣ����ų�B��
��[$\frac{��}{4}$��$\frac{��}{2}$]�ϣ�2x��[$\frac{��}{2}$����]����g��x����[$\frac{��}{4}$��$\frac{��}{2}$]�ϵļ����������ų�C��
��x��[$\frac{��}{6}$��$\frac{2��}{3}$]ʱ��2x��[$\frac{��}{3}$ $\frac{4��}{3}$]����2x=��ʱ��g��x��=2cos2xȡ����СֵΪ-2��
��2x=$\frac{��}{3}$ʱ��g��x��=2cos2xȡ�����ֵΪ1���ʺ��� g��x����ֵ��Ϊ[-2��1]��
��ѡ��D��
���� ������Ҫ�������Һ����������ԣ�����y=Asin����x+�գ���ͼ��任���ɣ����Һ�����ͼ��ĶԳ��ԣ����Һ����ĵ����ԡ��������ֵ�������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ABC-A1B1C1�У�P��Q�ֱ���AA1��B1C1�ϵĵ㣬��AP=3A1P��B1C1=4B1Q��
��ͼ����ֱ������ABC-A1B1C1�У�P��Q�ֱ���AA1��B1C1�ϵĵ㣬��AP=3A1P��B1C1=4B1Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��a��c | B�� | a��b��c | C�� | a��c��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��-1�� | B�� | ��1��3�� | C�� | ��1��-2����1��2�� | D�� | ��1��-1����1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
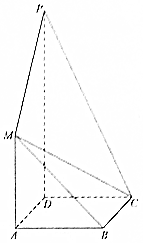 ��ͼ��������ABCD������AMPD���ڵ�ƽ�滥�ഹֱ��AD��PD��MA��PD��MA=AD=$\frac{1}{2}$PD=1��
��ͼ��������ABCD������AMPD���ڵ�ƽ�滥�ഹֱ��AD��PD��MA��PD��MA=AD=$\frac{1}{2}$PD=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com