
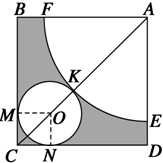
 如图所示,在边长为5+
如图所示,在边长为5+| 2 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
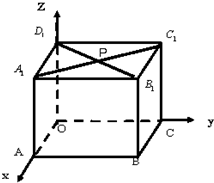 (1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.
(1)如图所示,在边长为2的正方体OABC-A1B1C1D1中,A1C1交B1D1于P.分别写出O、A、B、C、A1、B1、C1、D1、P的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在边长为4的正方形![]() 的边上有一点
的边上有一点![]() ,沿着折线
,沿着折线![]() 由
由![]() 点(起点)向
点(起点)向![]() 点(终点)移动,设
点(终点)移动,设![]() 点移动的路程为
点移动的路程为![]() ,
,![]() 的面积为
的面积为![]() .
.
 (1)求
(1)求![]() 的面积
的面积![]() 与点
与点![]() 移动的路程
移动的路程![]() 之间的关系式,并写出定义域;w.w.w.k.s.5.u.c.o.m
之间的关系式,并写出定义域;w.w.w.k.s.5.u.c.o.m ![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省郴州市高三下学期第六次月考理科数学 题型:解答题
(本小题满分13分)
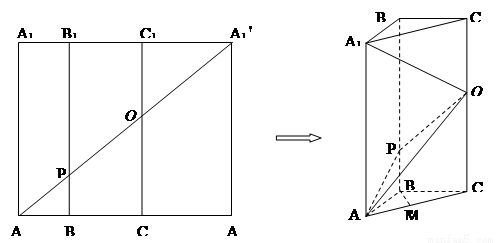
如图5所示 :在边长为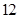 的正方形
的正方形 中,
中,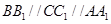 ,且
,且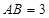 ,
,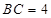 ,
,
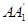 分别交
分别交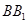 、
、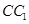 于
于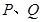 两点, 将正方形沿
两点, 将正方形沿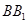 、
、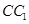 折叠,使得
折叠,使得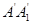 与
与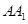 重合,
重合,
构成如图6所示的三棱柱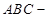
 .
.
( I )在底边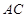 上有一点
上有一点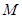 ,且
,且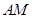 :
: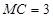 :
: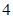 ,
求证:
,
求证: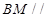 平面
平面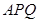 ;
;
( II )求直线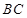 与平面
与平面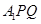 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
如图7所示,在边长为12的正方形![]() 中,
中,![]() ,且AB=3,BC=4,
,且AB=3,BC=4,![]() 分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得
分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得![]() 与AA1重合,构成如图5所示的三棱柱ABC—A1B1C1,请在图5中解决下列问题:
与AA1重合,构成如图5所示的三棱柱ABC—A1B1C1,请在图5中解决下列问题:
(1)求证:![]() ;
;
(2)在底边AC上有一点M,满足AM:MC=3:4,求证:BM//平面APQ。
(3)求直线BC与平面APQ所成角的正弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com