
【题目】已知三个点A(2,1),B(3,2),D(-1,4).
(1)求证:![]() ⊥
⊥![]() ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,则下列说法中不正确的是( )
A.由样本数据得到的回归方程![]() 必过样本点的中心
必过样本点的中心![]() .
.
B.残差平方和越小的模型,拟合的效果越好.
C.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 的值越小,说明模型的拟合效果越好.
的值越小,说明模型的拟合效果越好.
D.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为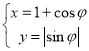 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值与最小值.
的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是函数
是函数![]() 定义域的一个子集,若存在
定义域的一个子集,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 的一个“准不动点”,也称
的一个“准不动点”,也称![]() 在区间
在区间![]() 上存在准不动点,已知
上存在准不动点,已知![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的准不动点;
的准不动点;
(2)若函数![]() 在区间
在区间![]() 上存在准不动点,求实数
上存在准不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁餐厅新店开业打算举办一次食品交易会,招待新老顾客试吃项目经理通过查阅最近5次食品交易会参会人数x(万人)与餐厅所用原材料数量y(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) | 13 | 9 | 8 | 10 | 12 |
原材料(袋) | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出y关于x的线性回归方程![]()
(2)已知购买原材料的费用C(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
参考公式: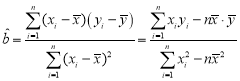 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com