
【题目】从某地区小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
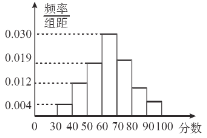
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该地区小学的这些学生中随机抽取3人,记这3人中成绩位于区间![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() ;(2)分布列详见解析,数学期望为1.8
;(2)分布列详见解析,数学期望为1.8
【解析】
(1)设区间![]() 内的频率为
内的频率为![]() ,则区间
,则区间![]() ,
,![]() 内的频率分别为
内的频率分别为![]() 和
和![]() ,再利用小矩形的面积和为1即可;
,再利用小矩形的面积和为1即可;
(2)从该小学的这些学生中随机抽取3人,相当于进行了3次独立重复试验.所以![]() 服从二项分布
服从二项分布![]() ,由频率分布直方图易得
,由频率分布直方图易得![]() ,再利用独立重复试验的概率公式计算即可得到答案.
,再利用独立重复试验的概率公式计算即可得到答案.
(1)设区间![]() 内的频率为
内的频率为![]() ,
,
则区间![]() ,
,![]() 内的频率分别为
内的频率分别为![]() 和
和![]() .
.
依题意得![]() ,解得
,解得![]() .
.
所以区间![]() 内的频率为
内的频率为![]() .
.
(2)从该小学的这些学生中随机抽取3人,相当于进行了3次独立重复试验.
所以![]() 服从二项分布
服从二项分布![]() ,其中
,其中![]() .
.
由(1)得,区间![]() 内的频率为
内的频率为![]() .
.
将频率视为概率得![]() .
.
因为![]() 的所有可能取值为0,1,2,3.
的所有可能取值为0,1,2,3.
且![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的数学期望为
的数学期望为![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点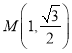 ,
,![]() 的参数方程为
的参数方程为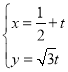 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
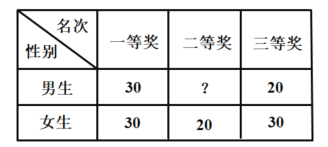
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
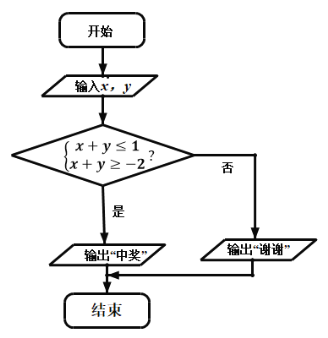
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受突如其来的新冠疫情的影响,全国各地学校都推迟2020年的春季开学.某学校“停课不停学”,利用云课平台提供免费线上课程.该学校为了解学生对线上课程的满意程度,随机抽取了500名学生对该线上课程评分.其频率分布直方图如下:若根据频率分布直方图得到的评分低于80分的概率估计值为0.45.
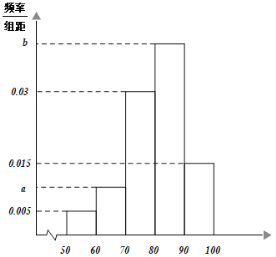
(1)(i)求直方图中的a,b值;
(ii)若评分的平均值和众数均不低于80分视为满意,判断该校学生对线上课程是否满意?并说明理由(同一组中的数据用该组区间的中点值为代表);
(2)若采用分层抽样的方法,从样本评分在[60,70)和[90,100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否存在?若存在,求直线
是否存在?若存在,求直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PAPD,E,F分别为AD,PB的中点.求证:
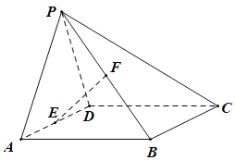
(1)EF//平面PCD;
(2)平面PAB平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学计划用他姓名的首字母![]() ,身份证的后4位数字(4位数字都不同)以及3个符号
,身份证的后4位数字(4位数字都不同)以及3个符号![]() 设置一个六位的密码.若
设置一个六位的密码.若![]() 必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的归家之一,某市为了制订合理的节水方案,对家庭用水情况进行了抽样调查,获得了某年100个家庭的月均用水量(单位:![]() )的数据,将这些数据按照
)的数据,将这些数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
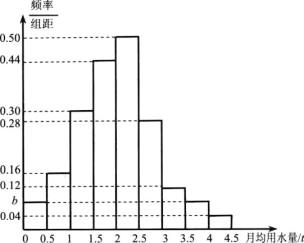
(1)求图中的![]() 值,若该市有30万个家庭,试估计全市月均用水量不低于
值,若该市有30万个家庭,试估计全市月均用水量不低于![]() 的家庭数;
的家庭数;
(2)假设同组中的每个数据都用该组区间的中点值代替,试估计全市家庭月均用水量的平均数;
(3)现从月均用水量在![]() ,
,![]() 的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在
的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在![]() 中的数量为
中的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com