


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:填空题
 ,则“
,则“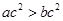 ”是“
”是“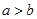 ”成立的充分不必要条件;
”成立的充分不必要条件;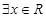 使得
使得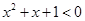 ”的否定是“
”的否定是“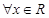 均有
均有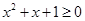 ”;
”;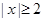 ,则
,则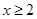 或
或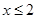 ”的否命题是“若
”的否命题是“若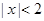 ,则
,则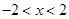 ”;
”;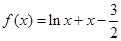 在区间
在区间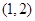 上有且仅有一个零点.
上有且仅有一个零点.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
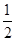 ,
,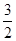 ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (填上所有正确结论得序号)
(填上所有正确结论得序号) ,若
,若 ,使得
,使得 ,则函数
,则函数 关于直线
关于直线 对称;
对称; 有2个零点;
有2个零点; 的不等式
的不等式 的解集为
的解集为 ,则
,则 ;
;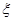 服从正态分布
服从正态分布 且
且 ,则
,则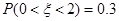 ;
; 的前
的前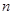 项和为
项和为 ,已知
,已知 ,则
,则
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 p1)∧(
p1)∧( p2);②p1∨(
p2);②p1∨( p2);③(
p2);③( p1)∧p2;④p1∧p2.
p1)∧p2;④p1∧p2.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.②③ | C.④ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.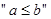 是 是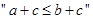 的充分不必要条件 的充分不必要条件 |
B.“已知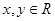 ,且 ,且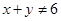 ,则 ,则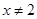 或 或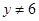 ”是真命题 ”是真命题 |
C.命题“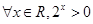 ”的否定是“ ”的否定是“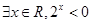 ” ” |
D.“若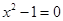 ,则 ,则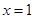 或 或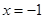 ”的否命题为“ ”的否命题为“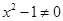 ,则 ,则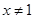 或 或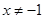 ” ” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com