
分析 (Ⅰ)求函数的导数,求得切线的斜率,利用曲线y=f(x)在点(1,f(1))处的切线与直线x-2y+1=0平行解方程可得a=1;
(2)求出g(x)和h(x)的导数,运用韦达定理和函数的零点的定义,化简整理,构造函数,运用导数判断单调性,即可得到所求最小值.
解答 解:(Ⅰ)∵f(x)=ln(x+a),定义域为(-a,+∞),
∴f′(x)=$\frac{1}{x+a}$,
∵曲线y=f(x)在点(1,f(1))处的切线与直线x-2y+1=0平行,
∴$\frac{1}{1+a}$=$\frac{1}{2}$,
∴a=1;
(Ⅱ)∵g(x)=f(x)+$\frac{1}{2}$x2-mx=lnx+$\frac{1}{2}$x2-mx,
∴g′(x)=$\frac{{x}^{2}-mx+1}{x}$,
令g′(x)=0,得x2-mx+1=0,
∵函数g(x)=f(x)+$\frac{1}{2}$x2-mx的极值点x1,x2(x1<x2)
∴x1+x2=m,x1•x2=1,
∴x1-x2=-$\sqrt{{m}^{2}-4}$
∵x1,x2(x1<x2)恰好是函数h(x)=f(x)-cx2-bx的零点,
即h(x)=f(x)-cx2-bx=lnx-cx2-bx=0由两个解分别为x1,x2,
∴h(x1)=lnx1-cx12-bx1=0,
h(x2)=lnx2-cx22-bx2=0,
两式相减ln$\frac{{x}_{1}}{{x}_{2}}$-c(x1+x2)(x1-x2)-b(x1-x2)=0,
∴b=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$-c(x1+x2)①
y=(x1-x2)h′($\frac{{x}_{1}+{x}_{2}}{2}$)=2•$\frac{\frac{{x}_{1}}{{x}_{2}}-1}{\frac{{x}_{1}}{{x}_{2}}+1}$-ln$\frac{{x}_{1}}{{x}_{2}}$,
令$\frac{{x}_{1}}{{x}_{2}}$=t(0<t<1),由x1+x2=m,x1x2=1可得t+$\frac{1}{t}$+2=m2,则t∈(0,$\frac{1}{4}$],
设函数G(t)=2•$\frac{t-1}{t+1}$-lnt,而G′(t)=-$\frac{(t-1)^{2}}{t(t+1)^{2}}$<0,
则y=G(t)在t∈(0,$\frac{1}{4}$]单调递减,
所以G(t)min=G($\frac{1}{4}$)=-$\frac{6}{5}$+ln4
所以y=(x1-x2)h′($\frac{{x}_{1}+{x}_{2}}{2}$)的最小值为-$\frac{6}{5}$+ln4.
点评 本题考查导数的运用:求切线的斜率、单调区间和最值,同时考查二次方程的韦达定理和函数的零点,考查运算求解能力,属于难题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
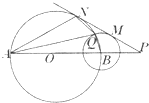 如图,以AB为直径的圆O与以N为圆心,半径为1的圆一个交点为Q,延长AB至点P,过点P作两圆的切线,分别切于M,N两点,已知AB=4.
如图,以AB为直径的圆O与以N为圆心,半径为1的圆一个交点为Q,延长AB至点P,过点P作两圆的切线,分别切于M,N两点,已知AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是边长为1的正方形,平面ADE⊥平面ABCD,DE⊥AD,BF∥DE,DE=BF=1,M为BC的中点.
如图,四边形ABCD是边长为1的正方形,平面ADE⊥平面ABCD,DE⊥AD,BF∥DE,DE=BF=1,M为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆O是△ABC的外接圆,AD垂直平分BC并交圆O于D点,直线CE与圆O相切于点C,与AB的延长线交于点E,BC=BE.
如图,圆O是△ABC的外接圆,AD垂直平分BC并交圆O于D点,直线CE与圆O相切于点C,与AB的延长线交于点E,BC=BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com